Angular Momentum Of A Point Mass
Muz Play
Apr 06, 2025 · 6 min read
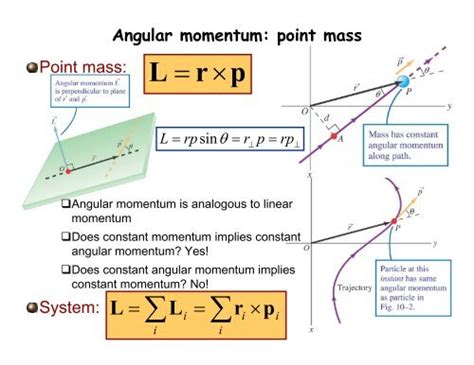
Table of Contents
Angular Momentum of a Point Mass: A Comprehensive Guide
Angular momentum, a crucial concept in physics, describes the rotational inertia of a system. Understanding it is key to grasping everything from the motion of planets around stars to the behavior of spinning tops. This article delves deep into the angular momentum of a point mass, exploring its definition, calculation, conservation, and applications.
Defining Angular Momentum
For a point mass, angular momentum is a measure of its tendency to continue rotating about a specific point or axis. Unlike linear momentum (mass times velocity), angular momentum considers both the mass and the distance from the axis of rotation. It's a vector quantity, meaning it has both magnitude and direction.
The formula for the angular momentum (L) of a point mass (m) moving with velocity (v) at a distance (r) from a chosen axis of rotation is:
L = r x p = r x mv
Where:
- r is the position vector from the axis of rotation to the point mass.
- p = mv is the linear momentum of the point mass.
- x denotes the cross product of two vectors.
The cross product ensures that angular momentum is a vector perpendicular to both the position vector and the linear momentum vector. The direction of the angular momentum vector is given by the right-hand rule: curl the fingers of your right hand from r to p, and your thumb points in the direction of L.
Understanding the Cross Product
The cross product is a crucial element in calculating angular momentum. For two vectors A and B, the magnitude of their cross product is:
|A x B| = |A| |B| sin θ
Where θ is the angle between the vectors A and B. This means that the angular momentum is zero when the velocity vector is parallel to the position vector (θ = 0° or 180°), indicating no rotation about that axis. The angular momentum is maximum when the velocity is perpendicular to the position vector (θ = 90°).
The cross product also determines the direction of the angular momentum vector. This directionality is essential in understanding rotational motion, as it dictates the sense of rotation (clockwise or counterclockwise).
Calculating Angular Momentum: Examples
Let's illustrate angular momentum calculations with a few examples:
Example 1: A Simple Circular Motion
Imagine a point mass of 2 kg moving in a circle of radius 1 meter with a constant speed of 4 m/s. To calculate the angular momentum about the center of the circle:
- Determine the linear momentum: p = mv = (2 kg)(4 m/s) = 8 kg m/s.
- Determine the position vector: The position vector is always perpendicular to the velocity vector in uniform circular motion. Its magnitude is the radius, 1 meter.
- Calculate the angular momentum: |L| = rp = (1 m)(8 kg m/s) = 8 kg m²/s. The direction of L is perpendicular to the plane of the circle, determined by the right-hand rule.
Example 2: Motion at an Angle
Consider a point mass of 1 kg moving with a velocity of 3 m/s at an angle of 30° to a position vector of length 2 meters.
- Resolve the velocity vector: The component of the velocity vector perpendicular to the position vector is v_perp = v sin θ = 3 m/s * sin(30°) = 1.5 m/s.
- Calculate the linear momentum perpendicular to the position vector: p_perp = m * v_perp = 1 kg * 1.5 m/s = 1.5 kg m/s.
- Calculate the angular momentum: |L| = r * p_perp = 2 m * 1.5 kg m/s = 3 kg m²/s. The direction is again determined by the right-hand rule.
Conservation of Angular Momentum
One of the most fundamental principles in physics is the conservation of angular momentum. In a closed system (where no external torques act), the total angular momentum remains constant. This means that if the moment of inertia changes, the angular velocity must adjust to maintain a constant angular momentum. This principle is crucial in various phenomena:
- Figure skater spinning: As a figure skater pulls their arms inwards, decreasing their moment of inertia, their angular velocity increases to conserve angular momentum.
- Rotating galaxies: The conservation of angular momentum plays a significant role in the formation and evolution of galaxies.
- Spinning tops: The stability of a spinning top is a direct consequence of the conservation of angular momentum.
External Torques and Angular Momentum Change
When an external torque acts on a system, the angular momentum changes. The rate of change of angular momentum is directly proportional to the net external torque acting on the system. This relationship is given by:
τ = dL/dt
Where:
- τ is the net external torque.
- dL/dt is the rate of change of angular momentum.
This equation is analogous to Newton's second law for linear motion (F = ma), where force causes a change in linear momentum.
Applications of Angular Momentum
The concept of angular momentum has wide-ranging applications across various fields:
- Astronomy: Angular momentum is crucial for understanding planetary orbits, stellar rotation, and the dynamics of galaxies.
- Classical Mechanics: It's fundamental to understanding the motion of rotating rigid bodies and systems of particles.
- Quantum Mechanics: Angular momentum is quantized at the atomic and subatomic levels, playing a pivotal role in atomic structure and spectroscopy.
- Engineering: The principles of angular momentum are applied in the design of gyroscopes, flywheels, and other rotating machinery.
Angular Momentum in Different Coordinate Systems
The calculation of angular momentum can be simplified by choosing an appropriate coordinate system.
1. Cartesian Coordinates: In this system, the angular momentum is calculated using the cross product formula directly, as shown earlier. This method is versatile but can become complex for systems with complicated geometries.
2. Cylindrical Coordinates: Cylindrical coordinates are particularly useful for systems exhibiting rotational symmetry about an axis. The angular momentum expression simplifies considerably in this system, focusing on the component of angular momentum along the axis of symmetry.
3. Spherical Coordinates: Spherical coordinates are ideal for analyzing systems with spherical symmetry. This system allows for a more concise representation of angular momentum, separating the radial and angular components of motion. This is especially useful in quantum mechanics where the angular momentum is quantized.
Advanced Concepts Related to Angular Momentum
While this article focuses on the angular momentum of a point mass, it's important to note more complex scenarios exist. These include:
- Angular Momentum of Extended Bodies: For objects that are not point masses, the angular momentum calculation becomes more involved, requiring integration over the entire mass distribution. The concept of the moment of inertia becomes crucial in this case.
- Rigid Body Rotation: The study of rigid body rotation requires understanding Euler's equations of motion, which describe the rotation of a rigid body under the influence of external torques.
- Precession and Nutation: These phenomena describe the complex motion of rotating bodies, often involving the interaction between angular momentum and external torques.
Conclusion
The angular momentum of a point mass is a fundamental concept with far-reaching implications. Understanding its definition, calculation, conservation, and applications provides a solid foundation for comprehending rotational motion in various physical systems. From the celestial dance of planets to the intricate mechanics of subatomic particles, angular momentum underpins the behavior of the universe around us. By grasping the principles discussed in this article, you'll develop a deeper appreciation for the elegant and powerful laws that govern our physical world. Further exploration into the advanced topics mentioned above will enrich your understanding of this fascinating and vital aspect of physics.
Latest Posts
Latest Posts
-
The Principle Of Conservation Of Matter States That Matter
Apr 08, 2025
-
Label The Structures Of The Upper Lateral Respiratory System
Apr 08, 2025
-
Standardization Of Naoh With Potassium Hydrogen Phthalate
Apr 08, 2025
-
Where Are The Transition Metals Located On The Periodic Table
Apr 08, 2025
-
How To Calculate Surplus And Shortage In Economics
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Angular Momentum Of A Point Mass . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.