Area Between Two Polar Curves Formula
Muz Play
Apr 02, 2025 · 5 min read
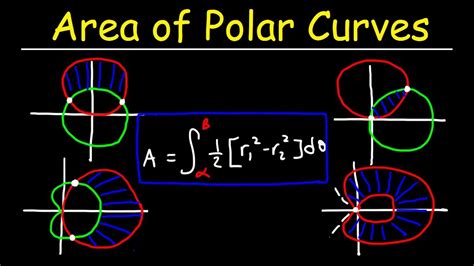
Table of Contents
Finding the Area Between Two Polar Curves: A Comprehensive Guide
Calculating the area enclosed by a single polar curve is a relatively straightforward process. However, determining the area between two polar curves requires a more nuanced approach. This comprehensive guide will walk you through the process, explaining the underlying formula, providing step-by-step examples, and offering tips for tackling complex scenarios. We'll explore various cases and provide practical strategies to help you master this important calculus concept.
Understanding Polar Coordinates
Before diving into the formula, let's refresh our understanding of polar coordinates. Instead of using Cartesian coordinates (x, y), polar coordinates represent a point using a distance (r) from the origin and an angle (θ) measured counterclockwise from the positive x-axis. The conversion between Cartesian and polar coordinates is given by:
- x = r cos(θ)
- y = r sin(θ)
Understanding this conversion is crucial for visualizing and working with polar curves.
The Area Formula for a Single Polar Curve
The foundation for finding the area between two polar curves lies in understanding how to calculate the area enclosed by a single polar curve. The area A enclosed by a curve r = f(θ) from θ = α to θ = β is given by the integral:
A = (1/2) ∫<sub>α</sub><sup>β</sup> [f(θ)]² dθ
This formula represents the accumulation of infinitesimally small triangular sectors, each with an area of (1/2)r²dθ. Integrating this expression over the desired range of θ yields the total area.
Deriving the Formula for the Area Between Two Polar Curves
Now, let's consider two polar curves, r₁ = f(θ) and r₂ = g(θ), where r₂ ≥ r₁ for α ≤ θ ≤ β. To find the area between these two curves, we simply subtract the area enclosed by the inner curve (r₁) from the area enclosed by the outer curve (r₂):
A = (1/2) ∫<sub>α</sub><sup>β</sup> ([g(θ)]² - [f(θ)]²) dθ
This formula elegantly captures the area between the two curves. The crucial aspect here is identifying the correct limits of integration (α and β) and ensuring that r₂ consistently represents the outer curve within the chosen interval.
Step-by-Step Examples:
Let's solidify our understanding with some practical examples.
Example 1: Simple Case
Find the area of the region that lies inside the cardioid r = 1 + cos(θ) and outside the circle r = 1.
1. Identify the Points of Intersection:
First, we need to find where the two curves intersect. Setting 1 + cos(θ) = 1, we get cos(θ) = 0, which implies θ = π/2 and θ = 3π/2.
2. Determine the Outer and Inner Curves:
For θ between π/2 and 3π/2, the cardioid (r = 1 + cos(θ)) is further from the origin than the circle (r = 1). Thus, r₂ = 1 + cos(θ) and r₁ = 1.
3. Apply the Formula:
The area is given by:
A = (1/2) ∫<sub>π/2</sub><sup>3π/2</sup> [(1 + cos(θ))² - 1²] dθ
Solving this integral (which involves trigonometric identities and integration techniques) yields the area.
Example 2: More Complex Scenario
Find the area of the region that lies inside both the curves r = 2cos(θ) and r = 2sin(θ).
1. Find the Points of Intersection:
Equating 2cos(θ) and 2sin(θ), we get tan(θ) = 1, which means θ = π/4 and θ = 5π/4. However, note that the curves are also at the origin (r=0) at θ = 0 and θ = π/2 for 2cos(θ) and at θ=π and θ=3π/2 for 2sin(θ).
2. Analyze the Curves:
In the interval [0, π/4], 2cos(θ) is the outer curve. In the interval [π/4, π/2], 2sin(θ) is the outer curve.
3. Split the Integral:
Because the outer curve changes, we need to split the integral into two parts:
A = (1/2) ∫<sub>0</sub><sup>π/4</sup> (2cos(θ))² dθ + (1/2) ∫<sub>π/4</sub><sup>π/2</sup> (2sin(θ))² dθ
Evaluating these two integrals and adding the results will give the total area.
Example 3: Handling Multiple Intersections
Some scenarios involve multiple intersections requiring careful segmentation of the integration. Visualizing the curves using graphing software can be immensely helpful in such situations. You might need to break the integral into multiple parts based on which curve is on the "outside" and which one is on the "inside" for different intervals of θ.
Advanced Considerations and Tips:
-
Symmetry: Utilize symmetry whenever possible to simplify calculations. If the region is symmetrical about the x-axis or y-axis, you can calculate the area of one half and then double the result.
-
Visual Aids: Sketching the curves is essential. Graphing tools (online or software-based) help visualize the intersection points and understand which curve is the outer and which is the inner within specific θ intervals.
-
Trigonometric Identities: Be prepared to use trigonometric identities to simplify integrands and make integration easier.
-
Numerical Methods: For complex integrals that are difficult or impossible to solve analytically, consider numerical integration methods (such as Simpson's rule or the trapezoidal rule).
-
Converting to Cartesian Coordinates: In some cases, converting the polar equations to Cartesian equations might simplify the problem, especially if the resulting Cartesian equations are easier to work with.
Conclusion: Mastering the Area Between Polar Curves
Finding the area between two polar curves is a powerful application of calculus that requires a solid grasp of polar coordinates and integration techniques. By carefully identifying intersection points, determining the outer and inner curves for each interval, and employing appropriate integration strategies, you can effectively calculate the area of even complex regions. Remember to leverage symmetry, utilize graphing tools, and don't hesitate to break the problem into manageable segments when needed. With practice, you’ll become adept at conquering these fascinating calculus challenges.
Latest Posts
Latest Posts
-
The Heterozygote Expresses Phenotype Of Both Homozygotes
Apr 03, 2025
-
Difference Between A Somatic Cell And A Gamete
Apr 03, 2025
-
Match The Structure Process To The Letter
Apr 03, 2025
-
Find The Basis Of The Subspace
Apr 03, 2025
-
Why Is Immersion Oil Used With The 100x Objective
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Area Between Two Polar Curves Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
