Choose The Most Likely Correlation Value For This Scatterplot
Muz Play
Apr 01, 2025 · 5 min read
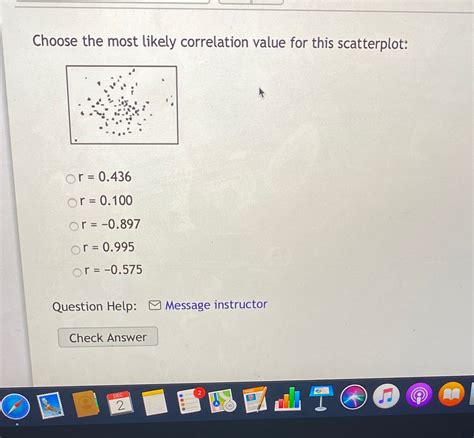
Table of Contents
Choose the Most Likely Correlation Value for This Scatterplot: A Comprehensive Guide
Scatterplots are powerful visual tools used in statistics to represent the relationship between two variables. Understanding how to interpret these plots, specifically identifying the correlation, is crucial for drawing meaningful conclusions from data. This article delves deep into the process of choosing the most likely correlation value for a given scatterplot, covering various correlation types, factors influencing correlation, and practical examples to enhance your understanding.
Understanding Correlation and Scatterplots
A scatterplot displays data points on a two-dimensional graph, with each point representing a pair of values for two variables. The pattern formed by these points reveals the nature of the relationship between the variables. This relationship is quantified using a correlation coefficient, often denoted by r.
Correlation refers to the statistical association between two variables. It describes the strength and direction of the linear relationship. The correlation coefficient ranges from -1 to +1:
- +1: Perfect positive correlation. As one variable increases, the other increases proportionally. The points on the scatterplot would lie perfectly along a straight upward-sloping line.
- 0: No linear correlation. There's no linear relationship between the variables. The points on the scatterplot would show no discernible pattern.
- -1: Perfect negative correlation. As one variable increases, the other decreases proportionally. The points on the scatterplot would lie perfectly along a straight downward-sloping line.
Values between -1 and +1 represent varying degrees of correlation. For instance, r = 0.8 indicates a strong positive correlation, while r = -0.5 indicates a moderate negative correlation.
Factors Influencing Correlation Values
Several factors can affect the correlation coefficient calculated from a scatterplot:
1. Linearity:
Correlation coefficients primarily measure linear relationships. If the relationship between variables is non-linear (e.g., curved), the correlation coefficient might be misleadingly low even if a strong relationship exists. Consider a parabolic relationship; the correlation coefficient might be close to zero, despite a clear pattern in the data.
2. Outliers:
Outliers, data points significantly distant from the overall pattern, can disproportionately influence the correlation coefficient. A single outlier can artificially inflate or deflate the correlation, making the calculated value less representative of the overall trend.
3. Range Restriction:
If the range of values for one or both variables is restricted, the correlation coefficient might underestimate the true strength of the relationship. For example, focusing on a narrow subset of data might obscure a stronger correlation that would be apparent with a wider range.
4. Sample Size:
The sample size influences the reliability of the correlation coefficient. A larger sample size generally leads to a more stable and reliable estimate of the population correlation. Smaller samples are more susceptible to sampling error, potentially leading to inaccurate correlation values.
Visual Interpretation of Scatterplots and Correlation
Accurately estimating the correlation from a scatterplot requires careful observation:
- Direction: Determine if the trend is upward (positive correlation) or downward (negative correlation).
- Strength: Assess the closeness of the points to a straight line. Tightly clustered points suggest a strong correlation, while scattered points indicate a weak correlation.
- Outliers: Identify any points significantly deviating from the overall pattern. These can heavily influence the perceived correlation.
Let's analyze different scenarios:
Scenario 1: Strong Positive Correlation
Imagine a scatterplot where the points are tightly clustered along a line that slopes upward from the bottom left to the top right. In this case, the most likely correlation value would be close to +1, perhaps around +0.8 or +0.9.
Scenario 2: Weak Negative Correlation
In a scatterplot with points loosely scattered around a downward-sloping line, the correlation would be negative but weak. A plausible correlation value might be around -0.3 or -0.4. The points are not tightly clustered, indicating a weaker relationship.
Scenario 3: No Correlation
A scatterplot where points are randomly scattered with no discernible pattern suggests no linear correlation. The correlation coefficient would be close to 0.
Scenario 4: Influence of Outliers
Consider a scatterplot showing a strong positive trend, but with a single point far away from the main cluster. This outlier could lower the overall correlation coefficient, even though the majority of points exhibit a strong positive relationship. The presence of outliers necessitates careful consideration when interpreting correlation values.
Practical Examples and Interpretation
Let's consider several hypothetical scatterplots and determine the most likely correlation values:
Example 1: A scatterplot showing the relationship between hours of study and exam scores. The points are tightly clustered along an upward-sloping line. Likely Correlation: +0.8 to +0.9 (strong positive correlation)
Example 2: A scatterplot depicting the relationship between ice cream sales and temperature. The points are clustered along an upward-sloping line, but with some scatter. Likely Correlation: +0.6 to +0.7 (moderate positive correlation)
Example 3: A scatterplot showing the relationship between age and reaction time. The points are loosely scattered around a downward-sloping line. Likely Correlation: -0.4 to -0.5 (moderate negative correlation)
Example 4: A scatterplot illustrating the relationship between shoe size and IQ. The points are randomly scattered with no clear pattern. Likely Correlation: Close to 0 (no correlation)
Example 5: A scatterplot representing the relationship between income and happiness. The points are somewhat clustered along an upward sloping line, but a few high-income individuals report lower happiness levels (outliers). Likely Correlation: +0.4 to +0.5 (moderate positive correlation), with the understanding that outliers may be influencing the value.
Advanced Considerations: Non-Linear Relationships and Transformations
As previously mentioned, the correlation coefficient only captures linear relationships. If the relationship between variables is non-linear (e.g., exponential, logarithmic, quadratic), the correlation coefficient might not accurately reflect the association. In such cases, data transformations (e.g., taking logarithms or square roots) might help linearize the relationship, allowing for a more meaningful correlation analysis.
Conclusion: Mastering Scatterplot Interpretation
Choosing the most likely correlation value for a scatterplot requires careful consideration of several factors. By understanding the concepts of correlation, linearity, outliers, and range restriction, you can effectively interpret scatterplots and draw accurate conclusions about the relationships between variables. Remember that visual inspection is a crucial first step, followed by a deeper analysis to account for potential confounding factors. This holistic approach will equip you with the skills to interpret scatterplots with confidence and extract meaningful insights from your data. The examples provided offer a practical framework for improving your ability to accurately assess correlation strength and direction directly from the visual representation of the data. Remember that practice makes perfect, so continue analyzing different scatterplots to hone your skills.
Latest Posts
Latest Posts
-
Difference Between Applied And Basic Science
Apr 03, 2025
-
Identify The Characteristics Of A Spontaneous Reaction
Apr 03, 2025
-
How To Find Average Acceleration From Acceleration Time Graph
Apr 03, 2025
-
Who Is The First Person To See Cells
Apr 03, 2025
-
Which Of The Following Are Examples Of Homologous Structures
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Choose The Most Likely Correlation Value For This Scatterplot . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
