Derivative Of A Constant Is 0
Muz Play
May 10, 2025 · 6 min read
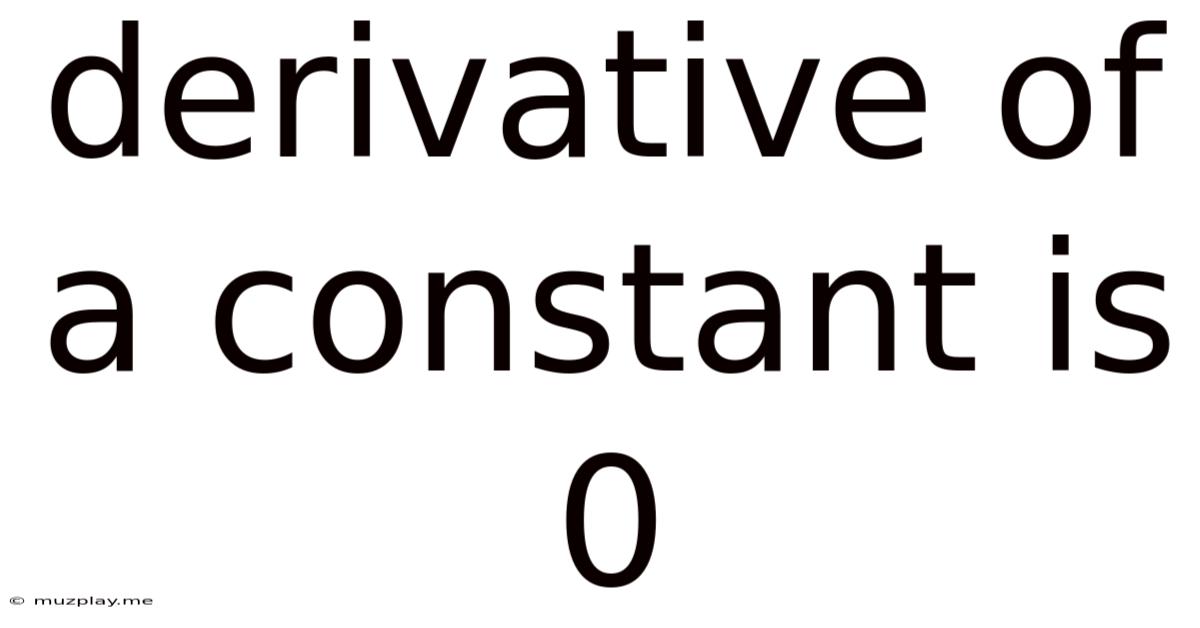
Table of Contents
The Derivative of a Constant is Zero: A Comprehensive Guide
The statement "the derivative of a constant is zero" is a fundamental concept in calculus. Understanding why this is true is crucial for mastering differentiation and its applications across various fields, from physics and engineering to economics and finance. This comprehensive guide will delve into this principle, exploring its proof, implications, and practical applications with numerous examples.
Understanding Derivatives
Before diving into the proof, let's refresh our understanding of derivatives. The derivative of a function at a point represents the instantaneous rate of change of that function at that specific point. Geometrically, it represents the slope of the tangent line to the curve of the function at that point. We denote the derivative of a function f(x) with respect to x as f'(x) or df/dx.
The derivative is calculated using the limit definition:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
This formula essentially calculates the slope of the secant line between two points on the curve, and as the distance between the points approaches zero (h→0), the slope of the secant line approaches the slope of the tangent line, giving us the instantaneous rate of change.
Proving the Derivative of a Constant is Zero
Now, let's prove that the derivative of a constant function is always zero. Let's consider a constant function f(x) = c, where c is any real number. Applying the limit definition of the derivative:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
Since f(x) = c for all x, we have f(x + h) = c as well. Substituting this into the limit definition:
f'(x) = lim (h→0) [(c - c) / h] = lim (h→0) [0 / h] = lim (h→0) 0 = 0
The expression simplifies to zero because the numerator is always zero, regardless of the value of h. Therefore, the limit is 0, proving that the derivative of a constant function is always zero.
This result makes intuitive sense. A constant function represents a horizontal line. The slope of a horizontal line is always zero. Since the derivative represents the slope of the tangent line, the derivative of a constant function must be zero.
Implications and Applications
The fact that the derivative of a constant is zero has profound implications across various mathematical concepts and practical applications.
1. Simplifying Derivatives
This rule significantly simplifies the process of differentiating complex functions. When dealing with functions that include constant terms, we can immediately eliminate those terms during differentiation. For example:
- f(x) = x² + 5: The derivative f'(x) = 2x. The constant '5' disappears.
- g(x) = 3x³ - 7x + 2: The derivative g'(x) = 9x² - 7. The constant '2' vanishes.
This simplification allows for more efficient calculations and problem-solving.
2. Integration and Indefinite Integrals
The derivative rule for constants plays a crucial role in integration. The process of integration is the reverse of differentiation. When we integrate a function, we are essentially finding a function whose derivative is the original function. Since the derivative of a constant is zero, any constant can be added to the result of an indefinite integral without changing its derivative. This is represented by the "+ C" term in indefinite integrals.
For example, if the integral of a function is x², the general solution is x² + C, where C is an arbitrary constant. This is because the derivative of x² + C is 2x, regardless of the value of C.
3. Optimization Problems
In optimization problems, which aim to find the maximum or minimum value of a function, the derivative is used to identify critical points – points where the derivative is zero or undefined. The derivative of a constant term does not affect the location of these critical points, focusing the optimization solely on the non-constant parts of the function.
4. Physics and Engineering
In physics and engineering, many applications involve describing motion, acceleration, and other dynamic systems. Constant terms often represent initial conditions (e.g., initial position, initial velocity). The fact that the derivative of a constant is zero implies that constant terms do not contribute to the rate of change of these quantities. For example, if the position of an object is given by s(t) = 5t² + 10, where 10 represents the initial position, the velocity (the derivative) is v(t) = 10t, ignoring the initial position term.
5. Economics and Finance
In economics and finance, many models involve functions representing costs, revenues, profits, or other economic variables. Constant terms might represent fixed costs or initial investments. Similar to physics and engineering, the derivative of a constant term is irrelevant when analyzing the marginal changes (rates of change) in economic quantities. For instance, if a cost function is given by C(x) = 5x + 1000, where 1000 is a fixed cost, the marginal cost (the derivative) is MC(x) = 5, focusing solely on the variable cost component.
Advanced Applications and Extensions
Beyond these basic applications, the concept extends to more complex scenarios:
-
Partial Derivatives: In multivariable calculus, partial derivatives consider the rate of change of a function with respect to one variable while holding other variables constant. The derivative of a constant term with respect to any variable is always zero.
-
Higher-Order Derivatives: The rule applies to higher-order derivatives as well. If you take the second, third, or any higher derivative of a constant, the result remains zero.
-
Implicit Differentiation: Even when dealing with implicit functions, where variables are intertwined, the derivative of a constant term remains zero.
Common Misconceptions and Pitfalls
While the concept itself is straightforward, some common mistakes can occur:
-
Confusing constants with variable coefficients: A constant is a fixed value; a coefficient is a value that might be constant within a specific problem but can vary in other contexts. Don't confuse the two.
-
Incorrectly applying the rule during complex differentiation: Ensure that you properly apply the chain rule, product rule, or quotient rule before simplifying expressions involving constants. The constant rule should only be applied after these other rules have been properly used.
Conclusion
The derivative of a constant is zero – a seemingly simple concept that underpins many crucial areas within calculus and its applications. Understanding this principle not only simplifies calculations but provides an intuitive understanding of how to analyze and interpret rates of change in various fields. Mastering this concept is fundamental to building a robust understanding of calculus and its widespread applications. Through consistent practice and a thorough grasp of the underlying principles, you can confidently apply this rule to a wide variety of problems and advance your mathematical skills.
Latest Posts
Latest Posts
-
The Collection Of All Possible Events Is Called
May 11, 2025
-
A Neutral Solution Has A Ph Of
May 11, 2025
-
A Nuclear Equation Is Balanced When
May 11, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of A Constant Is 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.