Electric Field Of A Disk Of Charge
Muz Play
Mar 28, 2025 · 5 min read
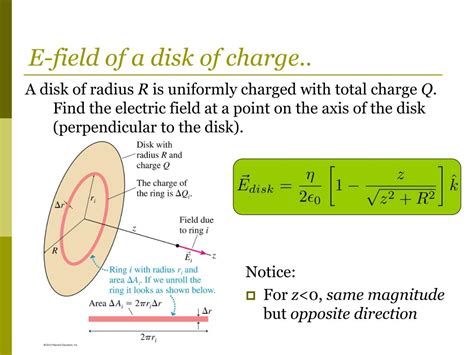
Table of Contents
Electric Field of a Disk of Charge: A Comprehensive Guide
The electric field, a fundamental concept in electromagnetism, describes the force experienced by a charged particle placed within its influence. Calculating the electric field for various charge distributions is a cornerstone of electrostatics. This article delves into the intricacies of calculating the electric field produced by a uniformly charged disk, providing a comprehensive understanding through detailed derivations, visualizations, and practical applications.
Understanding the Problem: Disk of Charge
Imagine a thin, flat disk with a uniform surface charge density, denoted by σ (sigma). This means that the charge is distributed evenly across the disk's surface area. Our goal is to determine the electric field at a point P located on the axis of symmetry of the disk, at a distance z from its center. This seemingly simple geometry presents a fascinating challenge in vector calculus, requiring a nuanced approach to integration.
Key Concepts and Assumptions
Before embarking on the derivation, let's clarify some crucial concepts and assumptions:
- Uniform Surface Charge Density (σ): The charge is distributed uniformly across the disk's surface. This simplifies the calculation significantly.
- Thin Disk: The thickness of the disk is negligible compared to its radius and the distance z. This allows us to treat the charge distribution as two-dimensional.
- Point P on the Axis of Symmetry: We're focusing on the electric field along the central axis perpendicular to the disk's plane. Calculating the field at off-axis points is significantly more complex.
- Coulomb's Law: The foundation of our calculation rests on Coulomb's Law, which describes the force between two point charges.
Deriving the Electric Field: A Step-by-Step Approach
To calculate the electric field, we'll employ a technique called integration. We'll divide the disk into infinitesimal charge elements, calculate the electric field contribution of each element, and then integrate over the entire disk to find the total field.
1. Defining the Infinitesimal Charge Element (dQ)
Consider a small ring of radius r and width dr on the disk. The area of this ring is given by dA = 2πrdr. Since the surface charge density is σ, the charge within this ring, dQ, is:
dQ = σ dA = σ(2πr dr)
2. Calculating the Electric Field due to dQ (dE)
The electric field (dE) at point P due to this infinitesimal charge element (dQ) can be determined using Coulomb's Law:
dE = k dQ / R²
where:
- k is Coulomb's constant (approximately 8.98755 × 10⁹ N⋅m²/C²)
- R is the distance between the charge element dQ and point P. By the Pythagorean theorem:
R = √(r² + z²)
The electric field dE is a vector quantity. Only the z-component of dE contributes to the total electric field along the axis of symmetry. The z-component of dE is:
dE<sub>z</sub> = dE cos θ = (k dQ / R²) (z / R) = k dQ z / R³ = k σ(2πr dr) z / (r² + z²)<sup>3/2</sup>
3. Integrating to Find the Total Electric Field (E)
To find the total electric field at point P, we need to integrate dE<sub>z</sub> over the entire disk, from r = 0 to r = R (the disk's radius):
E<sub>z</sub> = ∫ dE<sub>z</sub> = ∫<sub>0</sub><sup>R</sup> k σ(2πr dr) z / (r² + z²)<sup>3/2</sup>
This integral can be solved using substitution. Let u = r² + z², then du = 2r dr. The integral becomes:
E<sub>z</sub> = k σ π z ∫<sub>z²</sub><sup>R²+z²</sup> u<sup>-3/2</sup> du
Solving this integral, we obtain:
E<sub>z</sub> = k σ π z [ -2u<sup>-1/2</sup> ]<sub>z²</sub><sup>R²+z²</sup>
Simplifying and substituting back the limits of integration, we get:
E<sub>z</sub> = 2πkσ [ 1 - z / √(R² + z²) ]
This is the final expression for the electric field along the axis of symmetry of a uniformly charged disk.
Analyzing the Result: Understanding the Electric Field
The derived equation provides valuable insights into the electric field's behavior:
- Dependence on σ: The electric field is directly proportional to the surface charge density (σ). A higher charge density results in a stronger electric field.
- Dependence on z: The field's strength decreases as the distance z from the disk increases. This is intuitive – the farther away we are, the weaker the influence of the charge.
- Dependence on R: The radius of the disk (R) also influences the electric field. As R increases (for a constant z), the electric field approaches a limit.
- Limit as R → ∞: As the radius of the disk approaches infinity (while maintaining a constant σ), the expression simplifies to:
E<sub>z</sub> = 2πkσ
This is the electric field due to an infinite sheet of charge, a commonly encountered scenario in electrostatics.
Applications and Extensions
The concept of the electric field of a disk of charge has several applications:
- Modeling Charged Discs: This is crucial in understanding the electric fields of various physical systems that can be approximated as charged disks, such as capacitor plates or certain types of antennas.
- Approximating Larger Charged Objects: For large, flat charged objects, the disk model provides a reasonable approximation of the electric field near the surface.
- Electrostatic Lenses: The electric field from a disk of charge plays a significant role in designing electrostatic lenses used in electron optics and other applications.
Beyond the Axis of Symmetry: A More Complex Problem
Calculating the electric field at points off the axis of symmetry involves significantly more complex integration. This requires integrating over the entire disk using vector calculus techniques in two dimensions. While conceptually similar, the mathematical manipulations become far more challenging and typically involve double integrals. Numerical methods or advanced mathematical software are often employed for such calculations.
Conclusion: A Powerful Tool in Electrostatics
The calculation of the electric field due to a uniformly charged disk provides a powerful illustration of applying fundamental principles of electrostatics. The derivation, while involving calculus, reveals crucial relationships between the electric field and the disk's properties. Understanding this concept is vital for tackling more complex electrostatic problems and appreciating the intricacies of electric field distributions in various physical situations. From the simple model of a charged disk, we can extrapolate to understand more complex scenarios, demonstrating the enduring importance of this foundational concept within the broader field of electromagnetism. The detailed analysis presented herein equips readers with the knowledge and tools to confidently approach and interpret similar electrostatic problems, fostering a deeper understanding of this fascinating and fundamental aspect of physics.
Latest Posts
Latest Posts
-
Example Of A Line In A Poem
Mar 31, 2025
-
Interval Of Convergence Of A Taylor Series
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of A Disk Of Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
