Expected Number Of Trials Until Success
Muz Play
Apr 06, 2025 · 5 min read
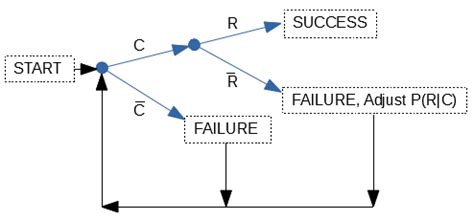
Table of Contents
Expected Number of Trials Until Success: A Deep Dive into Geometric Distribution
The concept of the expected number of trials until success is fundamental in probability theory and has wide-ranging applications across various fields. Understanding this concept is crucial for anyone working with probabilistic models, from data scientists analyzing experimental results to engineers assessing system reliability. This article provides a comprehensive exploration of this topic, covering its mathematical underpinnings, real-world examples, and variations.
Understanding the Geometric Distribution
At the heart of calculating the expected number of trials until success lies the geometric distribution. This probability distribution describes the probability of experiencing a certain number of failures before the first success in a sequence of independent Bernoulli trials. A Bernoulli trial is simply an experiment with only two possible outcomes: success or failure, where the probability of success remains constant for each trial.
Think of flipping a fair coin until you get heads. Each flip is a Bernoulli trial, with "heads" being success (probability 0.5) and "tails" being failure (probability 0.5). The geometric distribution helps us answer questions like: "What's the probability of getting the first heads on the third flip?" or "What's the average number of flips until we get heads?"
Key Characteristics of the Geometric Distribution:
- Independence: Each trial is independent of the others. The outcome of one trial does not influence the outcome of subsequent trials.
- Constant Probability: The probability of success (denoted as 'p') remains the same for every trial.
- Discrete: The random variable (number of trials until success) is discrete, meaning it can only take on integer values (1, 2, 3,...).
Calculating the Expected Number of Trials
The expected value (or mean) of a geometric distribution, representing the expected number of trials until the first success, is given by the simple formula:
E(X) = 1/p
Where:
- E(X) represents the expected number of trials until the first success.
- p is the probability of success in a single trial.
This formula tells us that the expected number of trials is inversely proportional to the probability of success. The higher the probability of success, the fewer trials we expect to perform before achieving success. Conversely, a lower probability of success implies a larger expected number of trials.
Example:
Let's return to the coin-flipping example. Since the probability of getting heads (success) is p = 0.5, the expected number of flips until we get heads is:
E(X) = 1/0.5 = 2
This means, on average, we expect to flip the coin twice before getting heads. It doesn't mean we'll always get heads on the second flip; sometimes we'll get it on the first, sometimes on the third, or even later. But the average number of flips over many repetitions will converge to 2.
Derivation of the Expected Value (For the Mathematically Inclined)
The expected value is calculated using the definition of expected value for a discrete random variable:
E(X) = Σ [x * P(X = x)] for all x
Where:
- x represents the number of trials until success (1, 2, 3,...).
- P(X = x) is the probability of needing exactly 'x' trials until success. This probability is given by the geometric probability mass function: P(X = x) = (1-p)^(x-1) * p
Substituting this into the expected value formula and using the sum of an infinite geometric series, we arrive at E(X) = 1/p. This derivation requires a good understanding of infinite series and summation techniques.
Real-World Applications
The concept of expected number of trials until success finds applications in diverse fields:
1. Quality Control: In manufacturing, the geometric distribution can model the number of items inspected before finding a defective one. Knowing the expected number of inspections helps determine optimal inspection strategies.
2. Clinical Trials: Suppose a new drug is being tested. The number of patients treated until a successful outcome (e.g., remission of a disease) is observed can be modeled using a geometric distribution. This information helps determine the sample size needed for the trial.
3. Search Algorithms: In computer science, algorithms often involve repeated attempts until a solution is found. The expected number of attempts can be modeled using the geometric distribution. This is relevant in areas like searching databases or solving optimization problems.
4. Sports: Consider the number of free throws a basketball player takes until they make one. Assuming a constant probability of success for each free throw, the geometric distribution can be used to model this situation.
5. Telecommunications: The number of times a signal is sent before successfully reaching the destination can be modeled by a geometric distribution, considering factors such as noise and signal attenuation.
Variations and Extensions
The basic geometric distribution assumes the probability of success remains constant across all trials. However, several variations exist:
1. Negative Binomial Distribution: This distribution generalizes the geometric distribution by considering the number of trials until r successes are observed, where r is a positive integer. The geometric distribution is a special case of the negative binomial distribution when r = 1.
2. Geometric Distribution with Varying Probabilities: If the probability of success changes from trial to trial, the geometric distribution no longer applies. More complex models are needed to handle this scenario.
3. Truncated Geometric Distribution: This distribution considers only a finite number of trials. For instance, if a maximum of 'n' trials are allowed, the distribution is truncated at 'n'.
Conclusion
The expected number of trials until success, deeply connected to the geometric distribution, is a powerful tool for modeling and analyzing a wide array of real-world phenomena involving repeated independent trials with a constant probability of success. Understanding this concept, along with its variations, provides valuable insights for decision-making in diverse fields, from quality control and clinical trials to computer science and telecommunications. The simplicity of its formula belies its profound implications in various probabilistic scenarios. Mastering this concept forms a strong foundation for more advanced studies in probability and statistics.
Latest Posts
Latest Posts
-
Worksheet Heating Curve Of Water Answers
Apr 08, 2025
-
How Many Atoms Are In A Fcc Unit Cell
Apr 08, 2025
-
Arc Length Formula For Polar Curves
Apr 08, 2025
-
What Are The Monomers And Polymers
Apr 08, 2025
-
Customary Units And Metric Units Chart
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Expected Number Of Trials Until Success . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.