Force On A Charge Moving In A Magnetic Field
Muz Play
Apr 03, 2025 · 6 min read
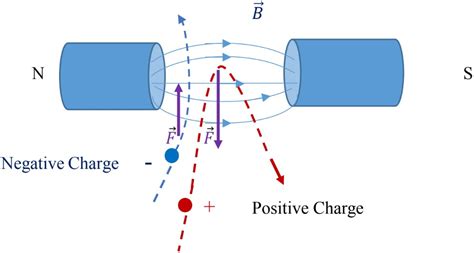
Table of Contents
Force on a Charge Moving in a Magnetic Field: A Comprehensive Guide
The interaction between moving charges and magnetic fields is a cornerstone of classical electromagnetism, with far-reaching implications in various fields, from electric motors to particle accelerators. Understanding the force exerted on a charge moving in a magnetic field is crucial for comprehending numerous phenomena and technological applications. This comprehensive guide delves into the fundamentals, exploring the underlying physics, mathematical formulations, and practical applications.
The Lorentz Force: The Fundamental Equation
The force experienced by a charged particle moving in a magnetic field is described by the Lorentz force law. This fundamental equation governs the interaction between charged particles and electromagnetic fields. It states that the force (F) on a charge (q) moving with velocity (v) in a magnetic field (B) is given by:
**F = q(v x B)
This equation reveals several key aspects:
- The force is proportional to the charge: A larger charge experiences a greater force.
- The force is proportional to the velocity: A faster-moving charge experiences a greater force. A stationary charge experiences no magnetic force.
- The force is proportional to the magnetic field strength: A stronger magnetic field results in a larger force.
- The force is perpendicular to both velocity and magnetic field: This crucial point is indicated by the cross product (x). The direction of the force is determined by the right-hand rule.
Understanding the Right-Hand Rule
The right-hand rule is essential for determining the direction of the Lorentz force. Imagine your right hand with your fingers pointing in the direction of the velocity vector (v) and then curling your fingers towards the direction of the magnetic field vector (B). Your thumb will then point in the direction of the force (F) acting on a positive charge. For a negative charge, the direction of the force is reversed.
Factors Affecting the Magnitude of the Force
The magnitude of the Lorentz force, denoted as |F|, is given by:
|F| = qvBsinθ
where θ is the angle between the velocity vector (v) and the magnetic field vector (B). This equation further clarifies the dependence of the force on the relative orientation of the velocity and the magnetic field:
- Maximum force: The force is maximum when the velocity and magnetic field are perpendicular (θ = 90°). In this case, |F| = qvB.
- Zero force: The force is zero when the velocity and magnetic field are parallel or antiparallel (θ = 0° or 180°). The charge moves along the magnetic field lines without experiencing any force.
Applications of the Lorentz Force
The Lorentz force is not merely a theoretical concept; it underpins numerous crucial technologies and natural phenomena:
1. Electric Motors
Electric motors rely fundamentally on the Lorentz force. A current flowing through a wire placed in a magnetic field experiences a force due to the movement of electrons in the wire. This force causes the wire to rotate, converting electrical energy into mechanical energy. The design and efficiency of motors are directly influenced by the principles of the Lorentz force.
2. Mass Spectrometers
Mass spectrometers utilize the Lorentz force to separate ions based on their mass-to-charge ratio. Ions are accelerated through a magnetic field, and the radius of their curvature depends on their mass-to-charge ratio. By measuring this curvature, the mass of the ions can be determined, allowing for the analysis of various materials and molecules.
3. Particle Accelerators
Particle accelerators, such as cyclotrons and synchrotrons, use magnetic fields to bend and accelerate charged particles to extremely high energies. The Lorentz force provides the centripetal force that keeps the particles moving in a circular path, allowing them to gain energy as they repeatedly pass through accelerating cavities.
4. Magnetic Resonance Imaging (MRI)
MRI machines exploit the interaction between nuclear spins and magnetic fields. The Lorentz force plays an indirect but significant role in manipulating the nuclear spins, leading to the production of detailed images of the human body.
5. Aurora Borealis and Aurora Australis
These breathtaking natural light displays are caused by charged particles from the sun interacting with Earth's magnetic field. The Lorentz force guides these particles towards the Earth's poles, where they collide with atmospheric gases, causing them to emit light.
The Force on a Charge Moving in Combined Electric and Magnetic Fields
In many practical situations, a charged particle experiences both electric (E) and magnetic (B) fields simultaneously. The total force acting on the charge is the sum of the electric force and the magnetic force, which is expressed by the complete Lorentz force equation:
F = qE** + q(v x B)
This equation encompasses the combined effects of electric and magnetic fields on a moving charge. The electric force is always along the direction of the electric field, while the magnetic force remains perpendicular to both the velocity and the magnetic field. The interplay between these forces can lead to complex trajectories for the charged particle.
Beyond Classical Physics: Relativistic Effects
At very high velocities approaching the speed of light, relativistic effects become significant. The classical Lorentz force equation needs modification to incorporate these relativistic corrections. This involves considering the relativistic mass increase of the particle and the transformation of fields under Lorentz transformations.
Mathematical Formalism and Advanced Concepts
A deeper understanding of the Lorentz force requires a more rigorous mathematical treatment, involving vector calculus and differential equations. This includes:
- Derivation of the Lorentz force from Maxwell's equations: The Lorentz force can be derived directly from Maxwell's equations, showcasing its fundamental role in electromagnetism.
- Solving equations of motion: Applying the Lorentz force equation to determine the trajectory of a charged particle under the influence of electric and magnetic fields often involves solving complex differential equations.
- Hamiltonian and Lagrangian formalisms: Advanced techniques such as Hamiltonian and Lagrangian mechanics can be employed to analyze the motion of charged particles in electromagnetic fields.
Conclusion: The Significance of the Lorentz Force
The force on a charge moving in a magnetic field, as described by the Lorentz force law, is a fundamental concept with profound implications across various domains of physics and engineering. Its understanding is crucial for comprehending the operation of numerous devices and natural phenomena. From the hum of an electric motor to the stunning beauty of the aurora borealis, the Lorentz force shapes our world in ways both subtle and spectacular. The continued exploration and refinement of its applications promise further advancements in technology and a deeper comprehension of the universe. Further study into the relativistic effects and the more complex mathematical frameworks can unlock even greater insights into the behaviour of charged particles in electromagnetic fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Force On A Charge Moving In A Magnetic Field . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
