How To Describe Distribution Of Data
Muz Play
Mar 31, 2025 · 6 min read
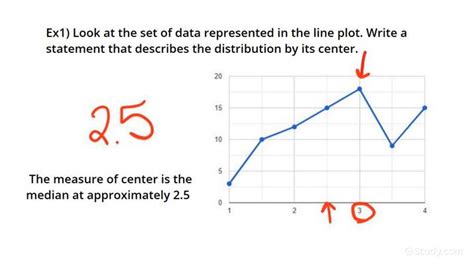
Table of Contents
How to Describe the Distribution of Data: A Comprehensive Guide
Understanding how to describe the distribution of data is a fundamental skill in statistics and data analysis. A data distribution reveals the underlying pattern of your data, providing crucial insights into its central tendency, spread, and shape. This comprehensive guide will walk you through various methods for describing data distributions, equipping you with the knowledge to effectively analyze and interpret your findings.
Why Describing Data Distribution Matters
Before diving into the methods, let's understand why describing data distribution is so crucial. Knowing the distribution of your data allows you to:
- Identify patterns and trends: Understanding the distribution helps reveal underlying patterns and trends within your dataset that might not be apparent through simple summary statistics.
- Make informed decisions: Accurate descriptions of data distributions are vital for making informed decisions based on data-driven insights. For example, understanding the distribution of customer ages can help tailor marketing strategies.
- Choose appropriate statistical tests: Many statistical tests rely on assumptions about the distribution of the data. Knowing the distribution allows you to select the most appropriate and valid statistical tests.
- Detect outliers and anomalies: Analyzing the distribution helps identify outliers or anomalies that may need further investigation or might require special handling in your analysis.
- Communicate findings effectively: Visualizing and describing the distribution of data allows you to effectively communicate your findings to a wider audience, regardless of their statistical background.
Methods for Describing Data Distribution
There are several key aspects of a data distribution to consider, and various methods for describing them. These include:
1. Measures of Central Tendency
Measures of central tendency describe the "center" of the data. The most common are:
- Mean: The average of all data points. It's sensitive to outliers.
- Median: The middle value when the data is sorted. It's less sensitive to outliers than the mean.
- Mode: The most frequent value in the dataset. A dataset can have multiple modes or no mode at all.
Choosing the right measure: The choice depends on the nature of your data and its distribution. For symmetrical distributions with no outliers, the mean is a good choice. For skewed distributions or those with outliers, the median is often preferred. The mode is useful for categorical data.
2. Measures of Dispersion (Spread)
Measures of dispersion describe how spread out the data is. Key measures include:
- Range: The difference between the maximum and minimum values. It's highly sensitive to outliers.
- Interquartile Range (IQR): The difference between the 75th percentile (Q3) and the 25th percentile (Q1). It's less sensitive to outliers than the range.
- Variance: The average of the squared differences from the mean. It provides a measure of the overall variability.
- Standard Deviation: The square root of the variance. It's expressed in the same units as the data, making it easier to interpret.
Interpreting the measures: A larger range, IQR, variance, or standard deviation indicates greater dispersion or variability in the data.
3. Shape of the Distribution
The shape of the distribution describes the overall pattern of the data. Key characteristics include:
- Symmetry: A symmetrical distribution is one where the left and right halves are mirror images of each other. The mean and median are approximately equal.
- Skewness: Skewness measures the asymmetry of the distribution.
- Positive Skew: The tail extends to the right (higher values). The mean is typically greater than the median.
- Negative Skew: The tail extends to the left (lower values). The mean is typically less than the median.
- Kurtosis: Kurtosis measures the "tailedness" and peakedness of the distribution.
- Leptokurtic: A distribution with heavy tails and a sharp peak (higher kurtosis).
- Mesokurtic: A distribution with tails and peak similar to a normal distribution (kurtosis around 3).
- Platykurtic: A distribution with light tails and a flat peak (lower kurtosis).
Visualizing the shape: Histograms, box plots, and kernel density plots are powerful visual tools for assessing the shape of the distribution.
4. Visualizations
Visualizations are crucial for understanding data distributions. Key visualization techniques include:
- Histograms: Show the frequency distribution of a continuous variable. They provide a visual representation of the shape, central tendency, and spread of the data.
- Box Plots (Box and Whisker Plots): Show the median, quartiles, and outliers of the data. They are excellent for comparing distributions across different groups.
- Stem-and-Leaf Plots: A simple way to display the distribution of data, especially for smaller datasets. They show both the shape and the individual data points.
- Kernel Density Plots: Provide a smooth estimate of the probability density function of a continuous variable. They offer a more refined representation of the distribution than histograms.
- Scatter Plots: Useful for visualizing the relationship between two continuous variables. While not directly describing a single distribution, patterns in a scatter plot can inform about the underlying distributions.
Interpreting Data Distributions: Examples and Case Studies
Let's explore some examples to illustrate how to describe data distributions effectively.
Example 1: Exam Scores
Imagine you have a dataset of exam scores. You calculate the mean score to be 75, the median to be 78, and the mode to be 80. The standard deviation is 10, and the distribution is slightly negatively skewed, indicating a few students scored significantly lower than the majority. A histogram reveals a unimodal distribution with a slight tail towards the lower scores.
Example 2: House Prices
Consider a dataset of house prices in a particular neighborhood. You find a large range in prices, with some high-value properties skewing the mean upward. The median price might be a more representative measure of central tendency. A box plot could effectively visualize the spread and potential outliers in house prices. The distribution might be positively skewed, reflecting a higher concentration of houses at lower price points and a few expensive properties.
Example 3: Customer Age
Analyzing the age distribution of your customers could reveal valuable information for marketing strategies. The mean, median, and mode age will indicate the typical customer age. The standard deviation will show the age range of your customer base. A histogram will depict the distribution, helping you determine whether you need to target specific age groups with different marketing approaches. For example, a bimodal distribution could suggest two distinct customer segments requiring separate marketing campaigns.
Advanced Techniques: Exploring Non-Normal Distributions
Many statistical methods assume a normal (Gaussian) distribution. However, real-world data often deviates from normality. Understanding these deviations is vital.
- Transformations: Techniques like logarithmic, square root, or Box-Cox transformations can help normalize skewed distributions, making them suitable for methods that assume normality.
- Non-parametric methods: If data clearly does not follow a normal distribution, non-parametric statistical tests offer alternatives that do not rely on assumptions about the data's distribution.
Conclusion: The Power of Understanding Data Distribution
Describing the distribution of data is not just a statistical exercise; it's a critical step in gaining actionable insights from your data. By understanding central tendency, spread, shape, and employing appropriate visualization techniques, you can effectively analyze, interpret, and communicate your findings, paving the way for more informed decisions and a stronger understanding of the phenomena your data represents. Remember to always consider the context of your data and choose the methods that best suit its characteristics to ensure accurate and meaningful interpretations.
Latest Posts
Latest Posts
-
Part Ii Equilibria Involving Sparingly Soluble Salts
Apr 02, 2025
-
Adding Strong Acid To A Buffer
Apr 02, 2025
-
The Most Reactive Group In The Periodic Table
Apr 02, 2025
-
How To Write Quadratic Equation From Graph
Apr 02, 2025
-
How To Place A Condom Catheter
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Describe Distribution Of Data . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
