How To Find Average Molecular Speed
Muz Play
Apr 05, 2025 · 7 min read
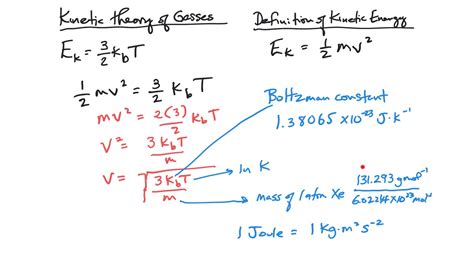
Table of Contents
How to Find Average Molecular Speed: A Comprehensive Guide
Determining the average molecular speed of a gas is a fundamental concept in physical chemistry with significant implications across various scientific disciplines. Understanding this concept allows us to better grasp gas behavior, reaction kinetics, and even atmospheric phenomena. This comprehensive guide will delve into the different methods and equations used to calculate the average molecular speed, explore the underlying principles, and provide practical examples to solidify your understanding.
Understanding Molecular Speed and its Distribution
Before diving into the calculations, it's crucial to understand what we mean by "average molecular speed." Gas molecules are in constant, chaotic motion, colliding with each other and the walls of their container. Their individual speeds vary significantly; some move rapidly, while others move more slowly. The average molecular speed is a statistical measure representing the typical speed of a molecule in the gas sample. It's important to note that this is not the speed of every single molecule, but rather a representative average.
The distribution of molecular speeds isn't uniform; it follows a specific probability distribution known as the Maxwell-Boltzmann distribution. This distribution describes the probability of finding a molecule with a particular speed at a given temperature. The curve is skewed to the right, indicating a larger number of molecules with speeds near the average, with a smaller number of molecules possessing very high or very low speeds.
Key Factors Affecting Average Molecular Speed
Several factors influence the average molecular speed of a gas:
1. Temperature:
Temperature is directly proportional to the average molecular speed. Higher temperatures lead to higher average speeds, as the increased thermal energy translates into faster molecular motion. This relationship is fundamental and is reflected in many of the equations used to calculate average molecular speed.
2. Molecular Mass (Molar Mass):
The molecular mass of the gas is inversely proportional to the average molecular speed. Lighter molecules move faster at the same temperature than heavier molecules. This is because lighter molecules require less energy to achieve the same kinetic energy as heavier molecules.
3. Pressure and Volume (Indirectly):
While not directly included in the most common equations, pressure and volume indirectly influence the average molecular speed through their impact on temperature. Changes in pressure and volume can alter the temperature of the gas, subsequently affecting the average molecular speed. For instance, compressing a gas adiabatically (without heat exchange) will increase its temperature and thus the average molecular speed.
Equations for Calculating Average Molecular Speed
Several equations can be used to determine the average molecular speed, each offering a slightly different perspective on this value:
1. Root-Mean-Square Speed (u<sub>rms</sub>):
The root-mean-square (rms) speed is the most commonly used measure of average molecular speed. It accounts for the fact that some molecules move much faster than others and provides a more representative average speed. The equation is:
u<sub>rms</sub> = √(3RT/M)
Where:
- u<sub>rms</sub> is the root-mean-square speed (m/s)
- R is the ideal gas constant (8.314 J/mol·K)
- T is the absolute temperature (in Kelvin)
- M is the molar mass of the gas (in kg/mol) - Note: It's crucial to use kg/mol for consistent units.
Example: Calculate the root-mean-square speed of oxygen (O<sub>2</sub>) molecules at 25°C (298 K). The molar mass of O<sub>2</sub> is 32 g/mol or 0.032 kg/mol.
u<sub>rms</sub> = √(3 * 8.314 J/mol·K * 298 K / 0.032 kg/mol) ≈ 482 m/s
2. Average Speed (u<sub>avg</sub>):
The average speed is a simpler measure of average molecular speed, calculated as the arithmetic mean of the speeds of all molecules. It's slightly lower than the root-mean-square speed. The equation is:
u<sub>avg</sub> = √(8RT/πM)
Where:
- u<sub>avg</sub> is the average speed (m/s)
- R, T, and M are as defined above.
Example: Using the same values for oxygen (O<sub>2</sub>) as before:
u<sub>avg</sub> = √(8 * 8.314 J/mol·K * 298 K / (π * 0.032 kg/mol)) ≈ 444 m/s
3. Most Probable Speed (u<sub>mp</sub>):
The most probable speed represents the speed at which the maximum number of molecules are moving. It's the speed corresponding to the peak of the Maxwell-Boltzmann distribution. The equation is:
u<sub>mp</sub> = √(2RT/M)
Where:
- u<sub>mp</sub> is the most probable speed (m/s)
- R, T, and M are as defined above.
Example: Again, using the oxygen (O<sub>2</sub>) values:
u<sub>mp</sub> = √(2 * 8.314 J/mol·K * 298 K / 0.032 kg/mol) ≈ 395 m/s
Relationship between Different Average Speeds
Notice that the three average speeds (u<sub>rms</sub>, u<sub>avg</sub>, u<sub>mp</sub>) are related and are always in the following order:
u<sub>rms</sub> > u<sub>avg</sub> > u<sub>mp</sub>
This reflects the shape of the Maxwell-Boltzmann distribution, with the rms speed being higher due to the influence of the faster-moving molecules.
Applications and Significance of Average Molecular Speed
The concept of average molecular speed has wide-ranging applications in various fields:
-
Reaction Kinetics: The rate of chemical reactions in gases is directly influenced by the frequency and energy of molecular collisions, which are directly related to the average molecular speed. Faster molecules lead to more frequent collisions and thus faster reaction rates.
-
Diffusion and Effusion: The rate of diffusion (the spreading of a gas) and effusion (the escape of a gas through a small hole) are directly proportional to the average molecular speed. Lighter gases diffuse and effuse faster than heavier gases. Graham's Law of Effusion is a direct consequence of this principle.
-
Atmospheric Science: Understanding average molecular speeds is essential for modeling atmospheric processes, including the distribution of gases in the atmosphere, the formation of clouds, and the behavior of pollutants.
-
Material Science: The average molecular speed influences the properties of materials, especially in the context of gases adsorbed on surfaces or within porous materials.
-
Vacuum Technology: In vacuum systems, understanding the average molecular speed is critical for designing effective pumps and evaluating the performance of vacuum seals.
Beyond the Basics: Advanced Considerations
While the equations provided above are widely used, it's important to acknowledge certain limitations:
-
Ideal Gas Assumption: These equations rely on the ideal gas law, which assumes negligible intermolecular forces and molecular volume. At high pressures or low temperatures, these assumptions break down, and the calculated average speeds may deviate from reality. More complex equations that account for real gas behavior would be necessary in such scenarios.
-
Non-Uniform Temperatures: The equations assume a uniform temperature throughout the gas sample. In situations with temperature gradients, the average molecular speed will vary spatially.
-
Molecular Interactions: The effect of intermolecular forces (attractive or repulsive) on molecular speeds is ignored in the basic equations. In real gases, these interactions can significantly influence the motion of molecules.
Conclusion: Mastering the Calculation of Average Molecular Speed
Calculating the average molecular speed of a gas is a fundamental skill in physical chemistry. This comprehensive guide has provided a clear explanation of the underlying principles, different methods of calculation (including root-mean-square, average, and most probable speed), practical examples, and insights into the significance of this concept across various scientific domains. While the ideal gas assumptions inherent in the basic equations should be kept in mind, understanding these concepts lays a strong foundation for tackling more advanced topics in physical chemistry and related fields. Remember to always ensure consistent units (especially using kg/mol for molar mass) for accurate calculations. By mastering these techniques, you will be better equipped to analyze and interpret the behavior of gases and their impact on a wide range of phenomena.
Latest Posts
Latest Posts
-
The Muscle Tissue That Shows No Striations Is
Apr 06, 2025
-
The Originals Classic Readings In Western Philosophy
Apr 06, 2025
-
Why Is Cell Division Important For Unicellular And Multicellular Organisms
Apr 06, 2025
-
How To Do U Substitution With Definite Integrals
Apr 06, 2025
-
Membrane That Holds The Coils Of The Small Intestine Together
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How To Find Average Molecular Speed . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
