How To Find Center Of Data
Muz Play
Apr 06, 2025 · 5 min read
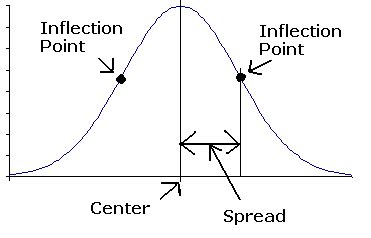
Table of Contents
How to Find the Center of Your Data: A Comprehensive Guide
Finding the center of your data is a crucial step in data analysis and understanding your dataset. It's the foundation for many statistical analyses and helps you visualize the distribution and characteristics of your data. This comprehensive guide will explore various methods for finding the center, their applications, and when to use each method. We'll delve into both numerical and graphical techniques, ensuring you have a robust understanding of this fundamental concept.
Understanding Measures of Central Tendency
Before diving into the methods, let's define what we mean by "center" in data analysis. We're referring to measures of central tendency, which are single values that attempt to describe a typical or central value in a dataset. These measures give you a concise summary of where the majority of your data points are clustered. The most common measures of central tendency are:
- Mean: This is the average value of the dataset. You calculate it by summing all values and dividing by the number of values. It's sensitive to outliers (extreme values).
- Median: This is the middle value when the data is arranged in ascending or descending order. If you have an even number of data points, the median is the average of the two middle values. It's less sensitive to outliers than the mean.
- Mode: This is the value that appears most frequently in the dataset. A dataset can have multiple modes or no mode at all. It's useful for categorical data and identifying the most common occurrence.
Calculating the Mean, Median, and Mode
Let's illustrate these calculations with a simple example:
Consider the following dataset representing the ages of participants in a workshop: 25, 30, 32, 35, 35, 40, 42, 45, 50, 55.
1. Mean:
Sum of ages: 25 + 30 + 32 + 35 + 35 + 40 + 42 + 45 + 50 + 55 = 389 Number of participants: 10 Mean age: 389 / 10 = 38.9
2. Median:
Arranging the ages in ascending order: 25, 30, 32, 35, 35, 40, 42, 45, 50, 55 Since there are 10 values (an even number), the median is the average of the two middle values (35 and 40): (35 + 40) / 2 = 37.5
3. Mode:
The age 35 appears twice, more frequently than any other age. Therefore, the mode is 35.
Choosing the Right Measure of Central Tendency
The best measure of central tendency depends on the nature of your data and the specific question you are trying to answer.
- Use the mean when: Your data is normally distributed (approximately symmetrical) and free from significant outliers. The mean provides a good representation of the typical value.
- Use the median when: Your data is skewed (not symmetrical) or contains outliers. The median is robust to outliers and provides a more representative measure of the center in such cases.
- Use the mode when: You are dealing with categorical data or want to identify the most frequent value in a numerical dataset.
Beyond the Basics: Weighted Averages and Grouped Data
In certain situations, you might need more advanced techniques to find the center of your data.
1. Weighted Average:
A weighted average assigns different weights to different data points based on their relative importance. For example, calculating a grade point average (GPA) involves a weighted average where different courses have different credit weights.
2. Grouped Data:
When dealing with large datasets, the data is often grouped into intervals or classes. Finding the mean for grouped data requires using the midpoint of each interval and multiplying it by the frequency of that interval.
Visualizing the Center: Histograms and Box Plots
Graphical representations can provide valuable insights into the center of your data and its distribution.
1. Histograms:
Histograms display the frequency distribution of your data. By looking at the histogram, you can visually identify where the data is concentrated, providing a visual estimate of the center. The peak of the histogram often corresponds to the mode.
2. Box Plots:
Box plots (also known as box-and-whisker plots) show the median, quartiles (values that divide the data into four equal parts), and potential outliers. The median is represented by the line inside the box, giving a clear visual indication of the central value.
Handling Outliers and Skewed Data
Outliers and skewed data can significantly impact the mean, making it a less reliable measure of the center. Here's how to address these challenges:
- Identify outliers: Use techniques like box plots or Z-scores to identify outliers.
- Transform your data: Consider data transformations (like logarithmic or square root transformations) to reduce skewness.
- Use robust measures: Employ the median instead of the mean as it's less sensitive to outliers.
- Trimmed mean: Calculate the mean after removing a certain percentage of the highest and lowest values.
Advanced Techniques: Geometric Mean and Harmonic Mean
Beyond the mean, median, and mode, there are other measures of central tendency suitable for specific data types.
1. Geometric Mean:
The geometric mean is useful when dealing with data that represents rates of change or multiplicative factors. It is calculated as the nth root of the product of n values. It's less sensitive to outliers than the arithmetic mean.
2. Harmonic Mean:
The harmonic mean is appropriate when dealing with rates or ratios, especially when dealing with reciprocals. It’s calculated as the reciprocal of the arithmetic mean of the reciprocals of the values.
Applications of Finding the Center of Data
Understanding the center of your data has numerous applications across diverse fields:
- Business Analytics: Identifying average customer spending, average transaction value, or average website visit duration.
- Finance: Determining average returns on investment, average risk, or average portfolio performance.
- Healthcare: Calculating average patient wait times, average hospital stay lengths, or average treatment costs.
- Science: Analyzing average experimental results, average temperatures, or average growth rates.
- Education: Determining average student test scores, average class sizes, or average graduation rates.
Conclusion
Finding the center of your data is a fundamental step in data analysis. Choosing the appropriate measure—mean, median, or mode—depends on the nature of your data and your research question. By understanding these methods and utilizing visual tools like histograms and box plots, you can gain valuable insights into your data's distribution and characteristics. Remember to consider outliers and skewness, and employ advanced techniques when necessary to accurately represent the center of your dataset. This comprehensive understanding equips you with the tools to perform robust and insightful data analysis.
Latest Posts
Latest Posts
-
Method Of Joints And Method Of Sections
Apr 08, 2025
-
How Is Artificial Selection Different From Genetic Engineering
Apr 08, 2025
-
Which Chamber Initially Receives Blood From The Systemic Circuit
Apr 08, 2025
-
What Does The Term Nonrepresentational Art Mean
Apr 08, 2025
-
Structures Within The Skin Called Arrector Pili Are
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find Center Of Data . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.