How To Find Ms Quantum Number
Muz Play
Mar 31, 2025 · 7 min read
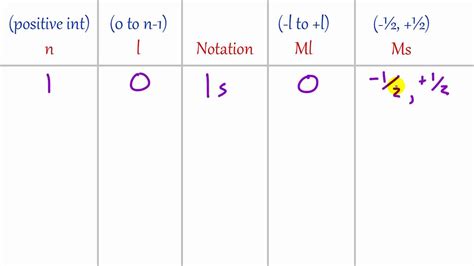
Table of Contents
How to Find the MS Quantum Number: A Comprehensive Guide
The magnetic spin quantum number (m<sub>s</sub>) is a crucial quantum number that describes the intrinsic angular momentum, or spin, of an electron within an atom. Understanding how to determine this number is fundamental to grasping atomic structure and predicting the behavior of electrons in various chemical and physical processes. This comprehensive guide will delve into the intricacies of the m<sub>s</sub> quantum number, explaining its significance, how to determine its value, and its relationship to other quantum numbers.
Understanding the Quantum Numbers
Before diving into the specifics of m<sub>s</sub>, let's briefly review the other three quantum numbers that describe an electron's state within an atom:
-
Principal Quantum Number (n): This number defines the electron shell and its energy level. It can take on positive integer values (n = 1, 2, 3...). Higher values of 'n' indicate higher energy levels and greater distance from the nucleus.
-
Azimuthal Quantum Number (l): Also known as the orbital angular momentum quantum number, 'l' determines the subshell and the shape of the electron's orbital. Its values range from 0 to n-1. l = 0 corresponds to an s orbital (spherical), l = 1 to a p orbital (dumbbell-shaped), l = 2 to a d orbital, and so on.
-
Magnetic Quantum Number (m<sub>l</sub>): This number specifies the orientation of the orbital in space relative to a magnetic field. It can take on integer values from -l to +l, including 0. For example, if l = 1 (p subshell), m<sub>l</sub> can be -1, 0, or +1, representing the three p orbitals (p<sub>x</sub>, p<sub>y</sub>, p<sub>z</sub>).
The Magnetic Spin Quantum Number (m<sub>s</sub>): A Deeper Dive
Unlike the other three quantum numbers which describe the electron's orbital motion, m<sub>s</sub> describes the intrinsic angular momentum, or spin, of the electron itself. It's a fundamental property, like mass or charge, and isn't dependent on the electron's position or orbital.
Imagine the electron as a tiny spinning sphere. While this is a simplified analogy, it helps visualize the concept of spin. This spinning creates a magnetic moment, meaning the electron behaves like a tiny magnet. The direction of this magnetic moment is what m<sub>s</sub> quantifies.
The crucial aspect of m<sub>s</sub> is its quantization. It can only take on two possible values:
- m<sub>s</sub> = +1/2: This represents the electron's spin being "up" (↑).
- m<sub>s</sub> = -1/2: This represents the electron's spin being "down" (↓).
These are often represented by arrows, as shown above. There's no value in between; the spin is either up or down. This quantization is a fundamental consequence of quantum mechanics.
How to Determine the m<sub>s</sub> Quantum Number
Determining the m<sub>s</sub> quantum number is remarkably straightforward. It is independent of the other quantum numbers (n, l, and m<sub>l</sub>). You don't need to perform any calculations; you simply need to know that each orbital can hold a maximum of two electrons, and these two electrons must have opposite spins.
The Pauli Exclusion Principle is the key here. This principle states that no two electrons in an atom can have the same set of four quantum numbers (n, l, m<sub>l</sub>, and m<sub>s</sub>). Therefore, if one electron in an orbital has m<sub>s</sub> = +1/2, the other electron in the same orbital must have m<sub>s</sub> = -1/2.
Steps to determine m<sub>s</sub>:
-
Identify the electron's orbital: Determine the values of n, l, and m<sub>l</sub> for the electron you're interested in. This information is usually provided or can be deduced from the electron configuration.
-
Apply the Pauli Exclusion Principle: If the orbital is already occupied by one electron, the second electron must have the opposite spin.
- If the first electron has m<sub>s</sub> = +1/2, the second electron will have m<sub>s</sub> = -1/2.
- If the first electron has m<sub>s</sub> = -1/2, the second electron will have m<sub>s</sub> = +1/2.
-
If the orbital is empty: You can assign either m<sub>s</sub> = +1/2 or m<sub>s</sub> = -1/2 to the electron. The choice is arbitrary, but consistency is key within a given electron configuration.
Examples: Finding m<sub>s</sub> in Different Scenarios
Let's illustrate this with some examples:
Example 1: Consider a helium atom (He). Its electron configuration is 1s². This means both electrons are in the 1s orbital (n=1, l=0, m<sub>l</sub>=0). One electron will have m<sub>s</sub> = +1/2, and the other will have m<sub>s</sub> = -1/2.
Example 2: Let's look at a nitrogen atom (N). Its electron configuration is 1s²2s²2p³. Consider the three electrons in the 2p subshell. Each of these electrons will occupy a different 2p orbital (m<sub>l</sub> = -1, 0, +1), and each will have m<sub>s</sub> = +1/2 or -1/2, as dictated by the Pauli Exclusion Principle. Each 2p orbital can only hold a maximum of two electrons with opposite spins.
Example 3: Consider the filling of orbitals in a more complex atom like iron (Fe). Iron has an electron configuration of [Ar] 3d⁶ 4s². Focus on the 3d orbitals. The first five electrons will fill each of the five 3d orbitals individually with a spin of +1/2 (following Hund's rule). The sixth electron will then pair up with one of the existing electrons, resulting in one orbital with two electrons having opposite spins. In this case, you’ll have various combinations of m<sub>s</sub> values, each dictated by the principle of filling orbitals.
The Significance of m<sub>s</sub>
The m<sub>s</sub> quantum number is not just a theoretical concept; it has profound implications in various fields:
-
Chemical Bonding: Electron pairing due to opposite spins (m<sub>s</sub> = +1/2 and m<sub>s</sub> = -1/2) is essential for the formation of covalent bonds.
-
Magnetic Properties: The magnetic moments associated with electron spins contribute to the overall magnetic properties of atoms and molecules, leading to phenomena like paramagnetism and ferromagnetism.
-
Spectroscopy: The splitting of spectral lines in the presence of a magnetic field (Zeeman effect) is directly related to the electron's spin and its m<sub>s</sub> value.
-
Nuclear Magnetic Resonance (NMR): NMR spectroscopy, a powerful technique used in chemistry and medicine, relies on the interaction between nuclear spins and external magnetic fields, which is influenced by the electron spin and thus m<sub>s</sub>.
-
Quantum Computing: The two spin states (+1/2 and -1/2) are fundamental to quantum computing, forming the basis of qubits, the fundamental units of information in quantum computers.
Beyond the Basics: Hund's Rule and Electron Configuration
While the determination of m<sub>s</sub> is straightforward, understanding its role within the broader context of atomic structure is crucial. Hund's rule plays a vital role in this context.
Hund's rule of maximum multiplicity states that electrons will individually occupy each orbital within a subshell before doubling up in any one orbital. This is because electrons with parallel spins (same m<sub>s</sub>) experience less electron-electron repulsion. This principle helps predict the electron configuration of atoms and molecules and therefore helps in determining individual m<sub>s</sub> values for electrons in their orbitals.
Conclusion
The magnetic spin quantum number (m<sub>s</sub>) is a fundamental property of electrons that describes their intrinsic angular momentum. Its two possible values, +1/2 and -1/2, are crucial for understanding atomic structure, chemical bonding, and various physical phenomena. Understanding how to determine m<sub>s</sub>, in conjunction with the other quantum numbers and principles like the Pauli Exclusion Principle and Hund's rule, is essential for a thorough understanding of atomic and molecular behavior. By applying the simple rules outlined above, you can successfully determine the m<sub>s</sub> quantum number for any electron within an atom's electronic structure.
Latest Posts
Latest Posts
-
Is Table Salt Homogeneous Or Heterogeneous
Apr 02, 2025
-
What Part Of Bacteria Cell Helps It Move
Apr 02, 2025
-
Is The Organic Layer On The Top Or Bottom
Apr 02, 2025
-
In A Solution It Is Dissolving Medium
Apr 02, 2025
-
How To Find Moles Of Naoh Used In Titration
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Find Ms Quantum Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
