If A Number Is Real Then It Is Also Rational
Muz Play
May 09, 2025 · 5 min read
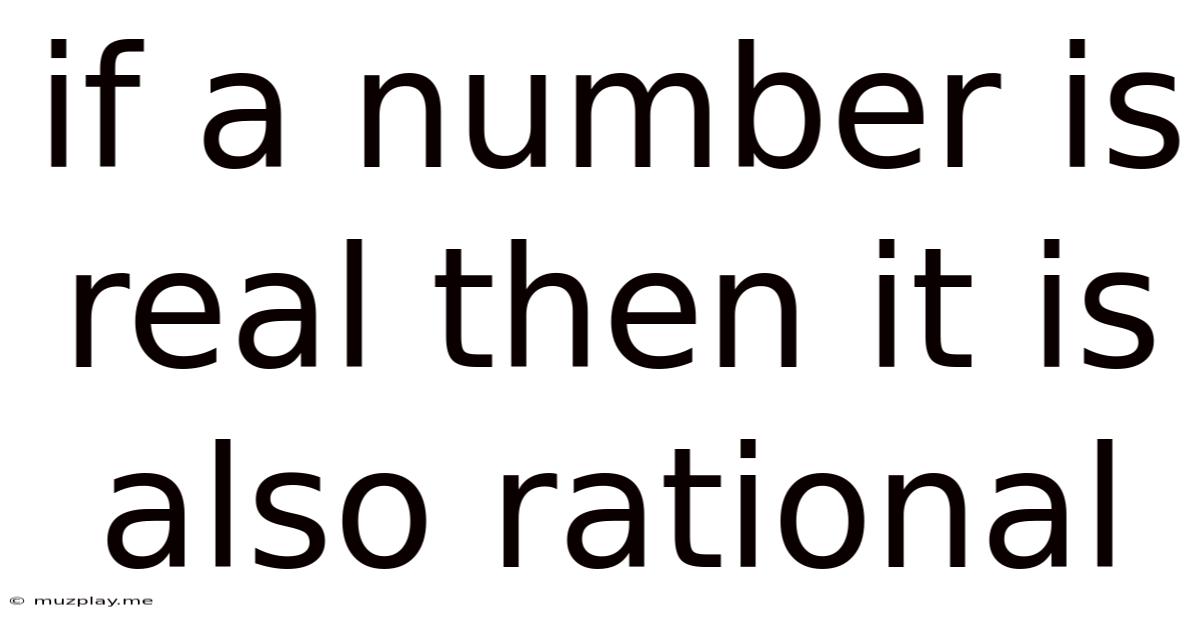
Table of Contents
The Falsehood of "If a Number is Real, Then it is Also Rational"
The statement "If a number is real, then it is also rational" is false. This is a fundamental concept in mathematics, distinguishing between the sets of real numbers and rational numbers. Understanding the difference is crucial for grasping various mathematical concepts and their applications. This article will delve into the definitions of real and rational numbers, explore examples that disprove the statement, and discuss the broader implications of this distinction.
Defining Real and Rational Numbers
Before we dissect the statement's fallacy, let's clearly define the terms involved.
Real Numbers: The set of real numbers encompasses all numbers that can be plotted on a number line. This includes:
-
Rational Numbers: Numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Examples include 1/2, -3/4, 0, and 7 (which can be expressed as 7/1).
-
Irrational Numbers: Numbers that cannot be expressed as a fraction of two integers. These numbers have decimal representations that neither terminate nor repeat. Famous examples include π (pi), approximately 3.14159..., e (Euler's number), approximately 2.71828..., and √2 (the square root of 2), approximately 1.41421...
The real numbers include both rational and irrational numbers. This means the set of real numbers is the union of the sets of rational and irrational numbers.
Rational Numbers: As mentioned above, rational numbers are those that can be written as a ratio of two integers. Their decimal representations either terminate (e.g., 0.75 = 3/4) or repeat (e.g., 0.333... = 1/3).
Counterexamples: Proving the Statement False
The statement "If a number is real, then it is also rational" is easily disproven by presenting just one irrational number. Since irrational numbers are a subset of real numbers, any irrational number serves as a counterexample.
Example 1: π (Pi)
Pi (π), the ratio of a circle's circumference to its diameter, is a real number. It's approximately 3.14159, but its decimal representation continues infinitely without repeating. This inherent non-repeating, non-terminating nature definitively classifies π as an irrational number. Therefore, π is a real number that is not rational, directly contradicting the original statement.
Example 2: √2 (Square Root of 2)
The square root of 2 (√2) is another classic example. It's a real number representing the length of the diagonal of a square with sides of length 1. It can be proven using proof by contradiction that √2 is irrational. Assume √2 is rational, meaning it can be expressed as p/q, where p and q are integers with no common factors. Squaring both sides leads to 2q² = p², implying p² is even, and therefore p is even. This leads to a contradiction, demonstrating that √2 cannot be expressed as a ratio of two integers. Thus, √2 is a real number that is not rational.
Example 3: e (Euler's Number)
Euler's number (e), the base of the natural logarithm, is approximately 2.71828. Like π, its decimal representation is infinite and non-repeating, making it an irrational number and, therefore, a real number that is not rational. The irrationality of e requires more advanced mathematical techniques to prove rigorously but is well-established within mathematics.
The Significance of the Distinction
The distinction between rational and irrational numbers is not merely a mathematical nicety; it has profound implications across various fields:
1. Calculus and Analysis: The concepts of limits, continuity, and derivatives rely heavily on the properties of real numbers, including both rational and irrational numbers. Irrational numbers are essential for understanding the behavior of functions at infinitesimally small intervals.
2. Geometry: Many geometric constructions involve irrational numbers. The diagonal of a unit square (√2), the circumference of a unit circle (2π), and the golden ratio (approximately 1.618), all irrational numbers, frequently appear in geometric calculations and constructions.
3. Number Theory: Number theory, the study of integers, extensively explores the properties of both rational and irrational numbers, including their distribution and relationships.
4. Computer Science: Representing real numbers in computers is a complex task. Since computers work with finite precision, irrational numbers are approximated using rational numbers with varying degrees of accuracy. Understanding the limitations of this approximation is crucial for accurate computations.
5. Physics and Engineering: Many physical constants, like the speed of light or the gravitational constant, are often represented as real numbers, including irrational numbers. Their accurate representation and calculations are essential for scientific modeling and engineering design.
Visualizing the Difference
Imagine a number line extending infinitely in both directions. Every point on this line represents a real number. The rational numbers are densely scattered throughout the line, but they are countable, meaning you could theoretically list them all (though it would take an infinitely long time). However, the irrational numbers are uncountable; there are infinitely more irrational numbers than rational numbers. This difference in cardinality is a significant mathematical result.
Conclusion: Understanding the Real Number System
The statement "If a number is real, then it is also rational" is demonstrably false. The existence of irrational numbers, which are a subset of real numbers, directly refutes it. The distinction between rational and irrational numbers is fundamental to mathematics, shaping our understanding of various mathematical branches and their applications in the sciences and engineering. Understanding this distinction is vital for appreciating the richness and complexity of the real number system, which forms the basis of much of modern mathematics and its applications. This nuanced understanding is crucial for anyone seeking a deeper grasp of mathematical principles and their applications in the broader world.
Latest Posts
Latest Posts
-
Select The Components Of The Eukaryotic Initiation Complex
May 09, 2025
-
Rusting Of Iron Is A Physical Or Chemical Change
May 09, 2025
-
Which Describes The Enthalpy Change Associated With An Endothermic Reaction
May 09, 2025
-
What Are Three Elements That Make Up Carbohydrates
May 09, 2025
-
Where Are Mhc Molecules Located On A Cell
May 09, 2025
Related Post
Thank you for visiting our website which covers about If A Number Is Real Then It Is Also Rational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.