Kinetic Energy Of An Ideal Gas
Muz Play
Mar 31, 2025 · 6 min read
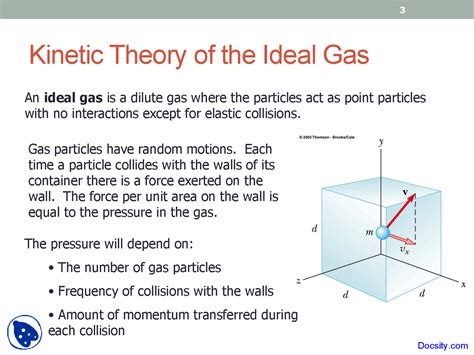
Table of Contents
Kinetic Energy of an Ideal Gas: A Deep Dive
The kinetic theory of gases provides a powerful framework for understanding the macroscopic properties of gases, such as pressure, temperature, and volume, by considering the microscopic behavior of individual gas molecules. A crucial concept within this theory is the kinetic energy of an ideal gas. Understanding this concept unlocks a deeper understanding of gas behavior and its relationship to thermodynamic principles. This article will delve into the kinetic energy of an ideal gas, exploring its derivation, implications, and connections to other thermodynamic properties.
What is Kinetic Energy?
Before diving into the kinetic energy of an ideal gas, let's refresh our understanding of kinetic energy in general. Kinetic energy is the energy an object possesses due to its motion. For a single particle with mass m and velocity v, the kinetic energy (KE) is given by the simple equation:
KE = ½mv²
This fundamental equation forms the cornerstone of our understanding of kinetic energy in various contexts, including the kinetic theory of gases.
The Ideal Gas Model
The ideal gas model simplifies the behavior of real gases by making several assumptions:
- Negligible intermolecular forces: Ideal gas molecules are assumed to exert no attractive or repulsive forces on each other. They only interact through elastic collisions.
- Negligible molecular volume: The volume occupied by the gas molecules themselves is negligible compared to the volume of the container.
- Random motion: Gas molecules are in constant, random motion. They move in straight lines until they collide with each other or the container walls.
- Elastic collisions: Collisions between gas molecules and the container walls are perfectly elastic, meaning no kinetic energy is lost during collisions.
These simplifications, while not perfectly reflecting the behavior of real gases, allow for a relatively straightforward mathematical treatment and provide a good approximation for many gases under specific conditions (low pressure and high temperature).
Average Kinetic Energy and Temperature
A key relationship in the kinetic theory of gases connects the average kinetic energy of gas molecules to the absolute temperature of the gas. This relationship is given by:
KE<sub>avg</sub> = (3/2)kT
Where:
- KE<sub>avg</sub> is the average kinetic energy per molecule
- k is the Boltzmann constant (approximately 1.38 x 10⁻²³ J/K)
- T is the absolute temperature in Kelvin
This equation is a fundamental result of the kinetic theory of gases. It reveals that the average kinetic energy of gas molecules is directly proportional to the absolute temperature. This means that as the temperature increases, the average speed of the gas molecules also increases. It's crucial to note that this refers to average kinetic energy; individual molecules will have varying kinetic energies due to their random motion.
Derivation of the Average Kinetic Energy Equation
The derivation of this equation involves considering the pressure exerted by a gas on the walls of its container. The pressure arises from the continuous bombardment of the walls by gas molecules. By analyzing the momentum transfer during these collisions and relating it to the macroscopic pressure, one can derive the relationship between average kinetic energy and temperature. The details of this derivation are often found in introductory physics and physical chemistry textbooks. It requires an understanding of statistical mechanics and the use of average values to account for the large number of molecules in a typical gas sample.
Distribution of Molecular Speeds
The random motion of gas molecules means they do not all have the same speed. Instead, their speeds follow a specific probability distribution known as the Maxwell-Boltzmann distribution. This distribution describes the fraction of molecules possessing a particular speed at a given temperature. The shape of the Maxwell-Boltzmann distribution depends on the temperature; at higher temperatures, the distribution is broader, indicating a wider range of molecular speeds.
The Maxwell-Boltzmann distribution is crucial because it allows us to calculate not just the average kinetic energy, but also other properties related to molecular speeds, such as the root-mean-square (rms) speed (v<sub>rms</sub>), the average speed (v<sub>avg</sub>), and the most probable speed (v<sub>p</sub>). These speeds are related to the temperature and the molar mass (M) of the gas through the following equations:
- v<sub>rms</sub> = √(3RT/M)
- v<sub>avg</sub> = √(8RT/πM)
- v<sub>p</sub> = √(2RT/M)
Where R is the ideal gas constant (8.314 J/mol·K). These equations further highlight the relationship between temperature and molecular speed.
Implications and Applications
The concept of kinetic energy in ideal gases has wide-ranging implications across various scientific disciplines.
1. Understanding Gas Behavior:
The kinetic energy of an ideal gas provides a microscopic explanation for macroscopic properties like pressure. Higher temperatures mean higher average kinetic energy, leading to more frequent and forceful collisions with the container walls, resulting in higher pressure.
2. Diffusion and Effusion:
The kinetic energy of gas molecules directly influences their rates of diffusion (mixing of gases) and effusion (escape of gas through a small hole). Lighter molecules with higher average speeds at a given temperature diffuse and effuse faster than heavier molecules. Graham's law of effusion is a direct consequence of this relationship.
3. Reaction Rates:
In chemical kinetics, the kinetic energy of reactant molecules is crucial in determining the rate of a reaction. Molecules must possess a minimum kinetic energy (activation energy) to overcome the energy barrier and undergo a reaction. Higher temperatures lead to a larger fraction of molecules possessing sufficient kinetic energy, thus increasing the reaction rate.
4. Thermodynamics:
The kinetic energy of an ideal gas is directly related to its internal energy (U). For a monatomic ideal gas, the internal energy is solely kinetic energy:
U = (3/2)nRT
where n is the number of moles of the gas. This relationship is fundamental in thermodynamics and is used in calculations involving heat transfer, work done by or on the gas, and changes in internal energy.
Limitations of the Ideal Gas Model
It's essential to acknowledge the limitations of the ideal gas model. Real gases deviate from ideal behavior at high pressures and low temperatures. At high pressures, the volume occupied by gas molecules becomes significant compared to the container volume, and intermolecular forces become increasingly important. At low temperatures, intermolecular attractive forces become more dominant, causing deviations from ideal behavior. Various equations of state, such as the van der Waals equation, have been developed to account for these deviations and model the behavior of real gases more accurately.
Conclusion
The kinetic energy of an ideal gas is a cornerstone concept in physical chemistry and thermodynamics. Its relationship to temperature, pressure, and other macroscopic properties provides a powerful framework for understanding the behavior of gases. While the ideal gas model simplifies the complexities of real gases, it provides a valuable approximation for many practical applications and offers a crucial stepping stone towards understanding more complex models of gas behavior. Further exploration into the Maxwell-Boltzmann distribution and the various equations of state provides a deeper appreciation of the intricacies of gas dynamics and the fundamental link between microscopic and macroscopic properties. The principles discussed here are fundamental to numerous scientific and engineering fields, highlighting the enduring importance of the kinetic theory of gases.
Latest Posts
Latest Posts
-
Is Table Salt Homogeneous Or Heterogeneous
Apr 02, 2025
-
What Part Of Bacteria Cell Helps It Move
Apr 02, 2025
-
Is The Organic Layer On The Top Or Bottom
Apr 02, 2025
-
In A Solution It Is Dissolving Medium
Apr 02, 2025
-
How To Find Moles Of Naoh Used In Titration
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Kinetic Energy Of An Ideal Gas . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
