Lattice Energy Is An Estimate Of The Bond .
Muz Play
Apr 07, 2025 · 8 min read
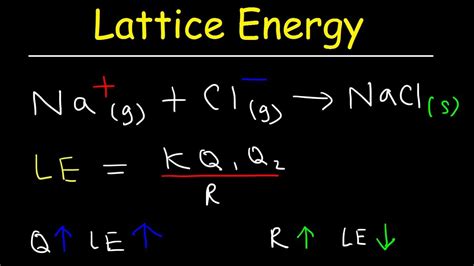
Table of Contents
Lattice Energy: An Estimate of the Strength of Ionic Bonds
Lattice energy is a crucial concept in chemistry, providing a quantitative measure of the strength of the ionic bonds within a crystalline solid. Understanding lattice energy allows us to predict and explain various properties of ionic compounds, such as their solubility, melting points, and reactivity. This article delves deep into the intricacies of lattice energy, exploring its definition, calculation methods, factors influencing its magnitude, and its applications in various fields.
What is Lattice Energy?
Lattice energy (U) is defined as the enthalpy change involved when one mole of an ionic compound is formed from its constituent gaseous ions. It's essentially the energy released when positive and negative ions come together to form a stable crystalline lattice structure. This energy is always exothermic, meaning energy is released during the process (U is a negative value). A more negative lattice energy indicates a stronger ionic bond and a more stable crystal lattice. Think of it as the "glue" holding the ions together in the solid state.
The Born-Haber Cycle: A Step-by-Step Approach
The direct measurement of lattice energy is experimentally challenging. Instead, chemists utilize the Born-Haber cycle, a thermodynamic cycle that allows for the indirect calculation of lattice energy. The cycle employs Hess's Law, which states that the total enthalpy change for a reaction is independent of the pathway taken. The Born-Haber cycle involves several steps, each with its associated enthalpy change:
-
Atomization of the metal: The enthalpy change of atomization (ΔH<sub>atom</sub>) represents the energy required to convert one mole of solid metal into gaseous metal atoms. This process is always endothermic.
-
Ionization of the metal: The ionization energy (IE) is the energy required to remove one or more electrons from a gaseous metal atom to form a gaseous metal cation. This is also endothermic.
-
Atomization of the non-metal: The enthalpy change of atomization of the non-metal (ΔH<sub>atom</sub>) is the energy required to convert one mole of the non-metal (usually a diatomic gas) into gaseous non-metal atoms. This is endothermic for diatomic molecules.
-
Electron affinity of the non-metal: The electron affinity (EA) is the energy change when one mole of gaseous non-metal atoms gains one or more electrons to form a gaseous anion. While often exothermic, it can be endothermic for some elements.
-
Formation of the ionic lattice: This step represents the formation of the ionic lattice from the gaseous ions, and its enthalpy change is the negative of the lattice energy (-U). This is the exothermic process we are trying to determine.
-
Overall enthalpy change of formation: The overall enthalpy change (ΔH<sub>f</sub>) is the enthalpy change for the formation of one mole of the ionic compound from its constituent elements in their standard states. This value can be experimentally determined.
By applying Hess's Law, the sum of the enthalpy changes for all these steps equals the overall enthalpy change of formation:
ΔH<sub>f</sub> = ΔH<sub>atom(metal)</sub> + IE + ΔH<sub>atom(non-metal)</sub> + EA - U
By rearranging the equation, we can calculate the lattice energy:
U = ΔH<sub>atom(metal)</sub> + IE + ΔH<sub>atom(non-metal)</sub> + EA - ΔH<sub>f</sub>
Factors Affecting Lattice Energy
Several factors significantly influence the magnitude of lattice energy. Understanding these factors helps predict the relative strength of ionic bonds in different compounds.
1. Charge of the Ions
The most significant factor influencing lattice energy is the charge of the ions. The greater the charges of the ions, the stronger the electrostatic attraction between them, and the higher the lattice energy (more negative). For instance, the lattice energy of MgO (Mg<sup>2+</sup> and O<sup>2-</sup>) is significantly greater than that of NaCl (Na<sup>+</sup> and Cl<sup>-</sup>).
2. Size of the Ions
The size of the ions also plays a crucial role. Smaller ions lead to a smaller interionic distance, resulting in stronger electrostatic attraction and a higher lattice energy. Conversely, larger ions lead to weaker attractions and lower lattice energy. This is because the electrostatic force is inversely proportional to the square of the distance between the ions (Coulomb's Law).
3. Crystal Structure
The arrangement of ions in the crystal lattice (crystal structure) influences lattice energy. Different crystal structures have different packing efficiencies, which affects the interionic distances and the overall energy of the lattice.
4. Madelung Constant
The Madelung constant (A) is a geometric factor that reflects the arrangement of ions in the crystal lattice. It accounts for the relative contributions of all ions in the lattice to the electrostatic attraction of a single ion. It is a dimensionless constant specific to a particular crystal structure, and its value reflects the efficiency of the packing of ions. A higher Madelung constant indicates a more efficient packing and therefore a higher lattice energy.
The Born-Landé Equation: A More Refined Calculation
The Born-Haber cycle provides an estimate of lattice energy. However, a more precise calculation can be obtained using the Born-Landé equation:
U = - (N<sub>A</sub>Mz<sup>+</sup>z<sup>-</sup>e<sup>2</sup>)/(4πε<sub>0</sub>r<sub>0</sub>)(1 - 1/n)
Where:
- N<sub>A</sub> is Avogadro's number
- M is the Madelung constant
- z<sup>+</sup> and z<sup>-</sup> are the charges of the cation and anion, respectively
- e is the elementary charge
- ε<sub>0</sub> is the permittivity of free space
- r<sub>0</sub> is the distance between the centers of adjacent ions
- n is the Born exponent, a measure of the compressibility of the ions
This equation accounts for the electrostatic interactions between ions and the repulsive forces that arise when the electron clouds of adjacent ions overlap. The Born exponent (n) is an empirical parameter that accounts for the repulsive forces, reflecting the hardness of the ions. The equation provides a more quantitative description of the factors affecting lattice energy.
Applications of Lattice Energy
Understanding lattice energy has several applications in diverse fields:
1. Predicting Properties of Ionic Compounds
Lattice energy helps predict properties such as melting points and boiling points. Compounds with high lattice energy tend to have high melting and boiling points, as more energy is required to overcome the strong electrostatic forces holding the ions together. Solubility in polar solvents is also influenced by lattice energy, with compounds having lower lattice energy tending to be more soluble.
2. Understanding Chemical Reactivity
Lattice energy plays a role in understanding the reactivity of ionic compounds. Compounds with lower lattice energy are more reactive as the ions are more easily separated and participate in chemical reactions. Conversely, compounds with high lattice energy are less reactive due to the strong ionic bonds.
3. Materials Science
Lattice energy is crucial in materials science for designing and synthesizing new materials with specific properties. The ability to predict and manipulate lattice energy allows for the creation of materials with desired characteristics, such as high thermal stability or specific optical properties. This is particularly relevant in the design of advanced ceramics, ionic conductors, and other functional materials.
4. Geochemistry
Lattice energy plays a significant role in understanding geochemical processes, like the formation and stability of minerals. The stability of a mineral is directly related to its lattice energy. Minerals with high lattice energy tend to be more stable and less prone to weathering or alteration. Understanding these relationships helps in predicting mineral formation and distribution in geological environments.
5. Environmental Chemistry
Lattice energy plays a role in understanding the environmental behavior of ionic compounds. For example, the solubility of ionic compounds in water is influenced by lattice energy. This influences their transport and fate in the environment, affecting soil fertility, water quality, and other environmental processes.
Beyond the Basics: Advanced Concepts
The discussion above provides a fundamental understanding of lattice energy. However, several advanced concepts further enhance our comprehension:
1. The Role of Polarization: Deviations from Ideal Ionic Behavior
The discussion so far assumes perfectly ionic compounds. However, in reality, there is always some degree of covalent character in ionic bonds, especially when there's a significant difference in electronegativity between the cation and anion. This covalent character affects the lattice energy. Polarization, the distortion of the electron cloud of an ion by the electric field of another ion, influences the strength of the bond and the lattice energy. Smaller, highly charged cations tend to polarize larger anions, leading to a partial covalent character and affecting the lattice energy calculation.
2. Lattice Defects and their Influence on Lattice Energy
Real crystals are not perfect; they contain defects like vacancies, interstitial atoms, and dislocations. These defects affect the overall energy of the lattice and subtly alter the lattice energy. While these effects are often small compared to the overall lattice energy, they can play a crucial role in influencing the properties of the material.
3. Temperature Dependence of Lattice Energy
Lattice energy is temperature-dependent, though the effect is generally small. At higher temperatures, the increased vibrational energy of the ions partially counteracts the electrostatic attraction, slightly reducing the effective lattice energy.
Conclusion
Lattice energy is a fundamental concept in chemistry that provides valuable insights into the strength of ionic bonds and the properties of ionic compounds. While the Born-Haber cycle and the Born-Landé equation offer ways to estimate and calculate lattice energy, understanding the influencing factors like charge, size, and crystal structure is crucial for predicting and interpreting the behavior of ionic materials. From predicting melting points to understanding geochemical processes and designing new materials, the concept of lattice energy plays a vital role in numerous scientific and technological applications. As our understanding of materials science and chemistry advances, the importance of lattice energy and its sophisticated applications will only continue to grow.
Latest Posts
Latest Posts
-
Which Structure Is Highlighted Nucleus Of Cardiac Muscle Fiber
Apr 09, 2025
-
Is Electric Conductor Acid Or Base
Apr 09, 2025
-
Practice Problems For Series And Parallel Circuits
Apr 09, 2025
-
Is Salt Water A Base Or Acid
Apr 09, 2025
-
State The Quadrant Of The Abdominopelvic Cavity Where The Pain
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Lattice Energy Is An Estimate Of The Bond . . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.