Number Of Atoms In Simple Cubic Unit Cell
Muz Play
Apr 04, 2025 · 6 min read
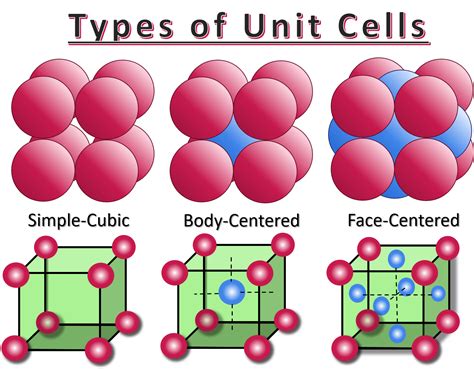
Table of Contents
Determining the Number of Atoms in a Simple Cubic Unit Cell: A Comprehensive Guide
The simple cubic (SC) unit cell is the simplest of the 14 Bravais lattices, forming the basis for understanding crystal structures in materials science and solid-state physics. Understanding how many atoms are present within a unit cell is fundamental to calculating density, determining various material properties, and comprehending the overall atomic arrangement. This article delves deep into the intricacies of determining the number of atoms in a simple cubic unit cell, exploring the underlying concepts and providing a detailed explanation.
Understanding Unit Cells and Crystal Lattices
Before diving into the calculation for a simple cubic unit cell, let's establish a firm foundation in crystallography. A crystal lattice is a three-dimensional arrangement of atoms, ions, or molecules in a highly ordered and repeating pattern. This pattern extends infinitely in all three spatial dimensions. A unit cell, on the other hand, is the smallest repeating unit of this lattice. It's like the building block that, when replicated in all directions, constructs the entire crystal structure. There are several different types of unit cells, each characterized by the arrangement of lattice points (locations of atoms) within them. The simple cubic unit cell is the most straightforward.
The Simple Cubic (SC) Unit Cell: A Visual Representation
Imagine a cube. In a simple cubic unit cell, atoms are located only at the corners of this cube. These corner atoms are shared by adjacent unit cells. This sharing is crucial when determining the number of atoms entirely within a single unit cell.
Visualizing Atom Sharing
Consider one corner atom. This atom is shared by eight adjacent unit cells—one for each corner of the cube where the atom resides. Consequently, only ⅛ of each corner atom is considered to belong to a single unit cell.
Calculating the Number of Atoms in a Simple Cubic Unit Cell
With the understanding of atom sharing in mind, the calculation becomes straightforward:
- Atoms per corner: 8 (one at each corner of the cube)
- Fraction of each corner atom within the unit cell: ⅛
- Total number of atoms within the unit cell: 8 corners × (⅛ atom/corner) = 1 atom
Therefore, a simple cubic unit cell contains exactly one atom. This is a crucial piece of information for various calculations involving density, packing efficiency, and other material properties.
Beyond the Simple Count: Implications and Applications
While the simple calculation reveals that there's only one atom per unit cell, this seemingly simple result has significant implications:
1. Packing Efficiency:
The simple cubic structure demonstrates a low packing efficiency. Packing efficiency refers to the percentage of the unit cell volume occupied by atoms. Because the atoms only occupy the corners and do not touch each other along the cube's edges, a significant amount of space remains empty within the unit cell. This contributes to its relatively low density compared to other crystal structures.
2. Density Calculations:
Knowing the number of atoms per unit cell is essential for determining the theoretical density of a material. The formula involves the mass of one atom (atomic mass divided by Avogadro's number), the unit cell volume (calculated from the lattice parameter), and the number of atoms within the unit cell (in this case, 1).
3. Understanding Material Properties:
The arrangement of atoms dictates many material properties, including mechanical strength, electrical conductivity, and thermal conductivity. The simple cubic structure, with its relatively large empty spaces and loose atomic packing, typically results in materials with lower strength and less efficient conductivity compared to structures with higher packing efficiencies, such as body-centered cubic (BCC) or face-centered cubic (FCC) structures.
4. X-ray Diffraction:
The simple cubic structure produces a characteristic diffraction pattern when subjected to X-ray diffraction analysis. The spacing between atomic planes in the crystal lattice influences the angles at which constructive interference occurs, which can be used to determine the lattice parameter and thus the unit cell dimensions.
Comparison with Other Cubic Crystal Structures
To further solidify the understanding of the simple cubic unit cell, it is beneficial to compare it with other cubic structures:
1. Body-Centered Cubic (BCC):
In a BCC structure, atoms are present at the corners of the cube, and one atom is located at the center of the cube. This results in a total of 2 atoms per unit cell (8 corner atoms × ⅛ + 1 center atom = 2 atoms). BCC structures generally exhibit better packing efficiency than SC structures.
2. Face-Centered Cubic (FCC):
An FCC structure has atoms at all eight corners and one atom in the center of each of the six faces of the cube. Each face-centered atom is shared by two unit cells, contributing ½ an atom to each cell. This results in a total of 4 atoms per unit cell (8 corner atoms × ⅛ + 6 face atoms × ½ = 4 atoms). FCC structures exhibit the highest packing efficiency among the cubic structures.
Advanced Considerations and Further Exploration
The seemingly simple concept of counting atoms in a unit cell can lead to more complex considerations:
1. Defects in Crystal Structures:
Real crystals often contain defects (such as vacancies, interstitial atoms, or dislocations) that deviate from the perfect, ideal arrangement described by the simple cubic model. These imperfections can significantly influence material properties.
2. Basis and Lattice:
In more sophisticated crystallography, the concept of a "basis" is introduced. The basis refers to a group of atoms associated with each lattice point. Thus, the simple cubic lattice might have a basis of one atom, while more complex structures can have multiple atoms per basis.
3. Space Groups:
Crystal structures are further classified according to their space group, which takes into account both the lattice and the symmetry operations that leave the crystal unchanged. The simple cubic structure belongs to a specific space group reflecting its cubic symmetry and atom arrangement.
Conclusion
Determining the number of atoms in a simple cubic unit cell, while seemingly simple at first glance, forms the bedrock for understanding numerous aspects of materials science and solid-state physics. The calculation (resulting in one atom per unit cell) is critical for calculating density, understanding packing efficiency, and analyzing diffraction patterns. By comparing the simple cubic structure with other cubic lattices (BCC and FCC), a broader appreciation for crystal structure's influence on material properties is gained. The exploration of defects, basis, and space groups provides a pathway for deeper investigation and understanding of the intricacies of crystalline materials. This fundamental knowledge lays the foundation for advanced studies in materials science and related fields.
Latest Posts
Latest Posts
-
Identify The Conditions For A Standard Electrochemical Cell
Apr 04, 2025
-
The Energy Of Activation Of A Reaction Is
Apr 04, 2025
-
Magnetic Field Of A Finite Wire
Apr 04, 2025
-
What Is The End Product Of Citric Acid Cycle
Apr 04, 2025
-
How To Find The Zeros Of A Function Algebraically
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Number Of Atoms In Simple Cubic Unit Cell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
