Potential And Kinetic Energy In A Pendulum
Muz Play
Mar 31, 2025 · 6 min read
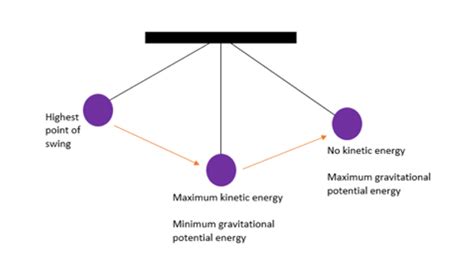
Table of Contents
Potential and Kinetic Energy in a Pendulum: A Deep Dive
The simple pendulum, a mass suspended from a fixed point by a string or rod, provides an elegant and readily observable demonstration of the interplay between potential and kinetic energy. Understanding this interplay is fundamental to grasping many concepts in physics, from mechanics to wave motion. This article will explore the potential and kinetic energy transformations within a pendulum, delving into the mathematical descriptions and practical applications of this classic physics system.
What is a Pendulum?
A pendulum, in its simplest form, consists of a bob (a mass) attached to a pivot point by a massless, inextensible string or rod. When displaced from its equilibrium position (vertical), the bob swings back and forth under the influence of gravity. The pendulum's motion is cyclical, repeating its swing until friction eventually brings it to rest. This seemingly simple system exhibits rich dynamics that reveal fundamental principles of physics.
Potential Energy in a Pendulum
Potential energy is the energy stored within an object due to its position or configuration. In the context of a pendulum, this is gravitational potential energy, the energy stored due to the bob's height above its lowest point. At its highest point in the swing (the amplitude), the bob possesses maximum potential energy and zero kinetic energy. As the bob swings down, this potential energy is converted into kinetic energy.
Calculating Gravitational Potential Energy
The gravitational potential energy (PE) of the pendulum bob is given by the formula:
PE = mgh
Where:
- m is the mass of the bob (in kg)
- g is the acceleration due to gravity (approximately 9.81 m/s² on Earth)
- h is the height of the bob above its lowest point (in meters)
The height 'h' can be expressed in terms of the pendulum's length (L) and the angle of displacement (θ) from the vertical using trigonometry:
h = L(1 - cos θ)
Therefore, a more complete expression for the potential energy is:
PE = mgL(1 - cos θ)
This equation shows that the potential energy is directly proportional to the mass, the acceleration due to gravity, the length of the pendulum, and the angle of displacement. A heavier bob, a stronger gravitational field, a longer pendulum, or a larger angle will all result in higher potential energy at the amplitude.
Kinetic Energy in a Pendulum
Kinetic energy is the energy of motion. As the pendulum bob swings downwards, its potential energy is converted into kinetic energy. At the bottom of its swing, the bob possesses maximum kinetic energy and zero potential energy (ignoring the slight height difference due to the bob's radius).
Calculating Kinetic Energy
The kinetic energy (KE) of the pendulum bob is given by the formula:
KE = ½mv²
Where:
- m is the mass of the bob (in kg)
- v is the velocity of the bob (in m/s)
The velocity of the bob at any point in its swing can be derived using conservation of energy principles, but a simpler, approximate expression can be used for small angles:
v ≈ √(2gL(1 - cos θ))
This approximation becomes less accurate as the angle of displacement increases. For larger angles, a more complex analysis using conservation of energy and the pendulum's angular velocity is necessary.
Substituting the velocity approximation into the kinetic energy equation gives:
KE ≈ mgL(1 - cos θ)
Conservation of Mechanical Energy in a Pendulum
In an ideal pendulum (without friction or air resistance), the total mechanical energy (the sum of potential and kinetic energy) remains constant throughout the swing. This principle of conservation of mechanical energy is expressed as:
Total Energy = PE + KE = constant
As the pendulum swings, there's a continuous exchange between potential and kinetic energy. At the highest point of the swing, the energy is entirely potential; at the lowest point, it's entirely kinetic. At any other point, the energy is a combination of both. This conservation provides a powerful tool for analyzing the pendulum's motion at any point along its trajectory.
Ideal vs. Real Pendulums
It's crucial to remember that the principle of conservation of energy applies perfectly only to an ideal pendulum. Real-world pendulums are affected by friction at the pivot point and air resistance, which dissipate energy as heat. Consequently, the amplitude of the pendulum's swing gradually decreases over time until it comes to rest. The lost mechanical energy is converted into other forms of energy, mainly heat.
The Period of a Pendulum
The period (T) of a pendulum is the time it takes to complete one full oscillation (one back-and-forth swing). For small angles of displacement, the period is approximately independent of the amplitude and is given by:
T ≈ 2π√(L/g)
This equation shows that the period is dependent only on the length of the pendulum (L) and the acceleration due to gravity (g). A longer pendulum has a longer period, while a stronger gravitational field results in a shorter period. This relationship is fundamental to the design and use of pendulum clocks, where the consistent period provides accurate timekeeping. For larger angles, this formula becomes less accurate, and the period becomes slightly longer. Higher order terms in the expansion of the period are needed to accurately account for large amplitude oscillations.
Applications of Pendulum Energy Transformations
The simple pendulum, despite its apparent simplicity, has numerous applications and provides insights into various physical phenomena:
-
Clocks: The consistent period of a pendulum, particularly in well-designed mechanisms, was exploited for centuries as the basis of accurate timekeeping devices.
-
Seismic Instruments: Pendulums are used in seismometers to measure ground motion during earthquakes, as their sensitivity to small displacements provides a reliable measurement.
-
Educational Demonstrations: The pendulum provides an excellent visual demonstration of the conservation of energy and the principles of oscillatory motion in physics education.
-
Mechanical Energy Conversion: The continuous conversion between potential and kinetic energy in a pendulum, though ultimately dissipative in a real system, provides a simple model for understanding energy transfer in other mechanical systems.
-
Physics Research: The pendulum's motion continues to be studied for its complexities in advanced physics, particularly concerning chaotic behavior and nonlinear dynamics at larger angles of displacement.
Advanced Considerations: Damped Oscillations and Chaos
The discussion above assumes an idealized frictionless pendulum. However, real-world pendulums experience damping due to air resistance and friction at the pivot point. This damping causes the amplitude of the pendulum's swing to decrease over time, eventually coming to rest. The equation of motion becomes more complex to account for this damping force.
Furthermore, at larger amplitudes, the pendulum's motion becomes increasingly nonlinear, exhibiting chaotic behavior under certain conditions. This means that even small changes in initial conditions can lead to significantly different trajectories over time. This nonlinearity and sensitivity to initial conditions make the analysis of large-amplitude pendulum motion far more challenging and fascinating. The simple harmonic motion approximation breaks down, requiring more advanced mathematical techniques like numerical methods to solve for the pendulum's trajectory.
Conclusion
The simple pendulum, though appearing elementary at first glance, serves as a rich source of learning about potential and kinetic energy transformations. The interplay between these two forms of energy, governed by the principles of conservation of energy (in the ideal case) and the effects of damping and nonlinearity in the real world, reveals fundamental principles of classical mechanics. From its historical use in timekeeping to its ongoing relevance in advanced physics research, the pendulum remains an indispensable tool for understanding the physical world. Its seemingly straightforward motion belies a depth of complexity that continues to fascinate and challenge physicists to this day. The exploration of potential and kinetic energy within a pendulum provides a solid foundation for tackling more advanced concepts in physics and engineering.
Latest Posts
Latest Posts
-
Why Is Water Necessary For Life
Apr 02, 2025
-
The Process Of Independent Assortment Refers To
Apr 02, 2025
-
Is Table Salt Homogeneous Or Heterogeneous
Apr 02, 2025
-
What Part Of Bacteria Cell Helps It Move
Apr 02, 2025
-
Is The Organic Layer On The Top Or Bottom
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Potential And Kinetic Energy In A Pendulum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
