Raising And Lowering Operators Angular Momentum
Muz Play
Mar 31, 2025 · 7 min read
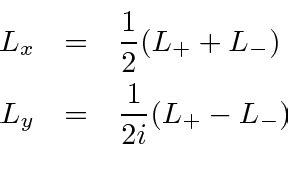
Table of Contents
Raising and Lowering Operators in Angular Momentum: A Comprehensive Guide
Angular momentum is a fundamental concept in quantum mechanics, describing the rotational motion of particles and systems. Understanding its mathematical representation and manipulation is crucial for comprehending various quantum phenomena. A key tool in this understanding lies in the use of raising and lowering operators, also known as ladder operators. This article provides a comprehensive exploration of these operators, detailing their properties, applications, and significance within the framework of angular momentum.
Understanding Angular Momentum in Quantum Mechanics
Before diving into raising and lowering operators, let's establish a firm foundation in the concept of angular momentum itself. In classical mechanics, angular momentum is defined as the cross product of the position vector and linear momentum. However, in the quantum realm, angular momentum takes on a more nuanced and abstract form.
It's represented by a vector operator, conventionally denoted as J, with three components: J<sub>x</sub>, J<sub>y</sub>, and J<sub>z</sub>. These components do not commute; that is, their order of operation matters. This non-commutativity is a defining characteristic of quantum angular momentum and leads to the concept of quantization.
The fundamental commutation relations for angular momentum are:
[J<sub>x</sub>, J<sub>y</sub>] = iħJ<sub>z</sub> [J<sub>y</sub>, J<sub>z</sub>] = iħJ<sub>x</sub> [J<sub>z</sub>, J<sub>x</sub>] = iħJ<sub>y</sub>
where ħ (h-bar) is the reduced Planck constant. These relations imply that you cannot simultaneously know the precise values of two different components of angular momentum. This is a direct consequence of the Heisenberg uncertainty principle.
Another crucial operator is the square of the total angular momentum, J², defined as:
J² = J<sub>x</sub>² + J<sub>y</sub>² + J<sub>z</sub>²
This operator commutes with each component of J:
[J², J<sub>x</sub>] = [J², J<sub>y</sub>] = [J², J<sub>z</sub>] = 0
This means that we can simultaneously measure the total angular momentum (J²) and one of its components, conventionally chosen as J<sub>z</sub>.
Introducing Raising and Lowering Operators: J+ and J-
The raising and lowering operators, J<sup>+</sup> and J<sup>-</sup>, are defined as linear combinations of J<sub>x</sub> and J<sub>y</sub>:
J<sup>+</sup> = J<sub>x</sub> + iJ<sub>y</sub> J<sup>-</sup> = J<sub>x</sub> - iJ<sub>y</sub>
These operators are incredibly powerful because they allow us to systematically move between different angular momentum states. Their action on an eigenstate of J<sub>z</sub> is to raise or lower its eigenvalue by ħ.
Let's consider an eigenstate |j, m⟩ of both J² and J<sub>z</sub>. The eigenvalues are given by:
J²|j, m⟩ = ħ²j(j+1)|j, m⟩ J<sub>z</sub>|j, m⟩ = ħm|j, m⟩
where 'j' is the total angular momentum quantum number (can be an integer or half-integer) and 'm' is the magnetic quantum number, ranging from -j to +j in integer steps.
The action of the raising and lowering operators is then:
J<sup>+</sup>|j, m⟩ = ħ√[(j-m)(j+m+1)]|j, m+1⟩ J<sup>-</sup>|j, m⟩ = ħ√[(j+m)(j-m+1)]|j, m-1⟩
These equations show that J<sup>+</sup> increases the m value by 1, while J<sup>-</sup> decreases it by 1. The square root factors are crucial; they ensure that the operators are properly normalized and that the process terminates at the maximum and minimum values of m.
Properties and Significance of Raising and Lowering Operators
The raising and lowering operators possess several crucial properties:
-
Ladder Operation: As their name suggests, they allow us to "climb" the ladder of angular momentum states, systematically changing the magnetic quantum number (m) while keeping the total angular momentum quantum number (j) constant.
-
Hermitian Conjugates: J<sup>+</sup> and J<sup>-</sup> are Hermitian conjugates of each other: (J<sup>+</sup>)<sup>†</sup> = J<sup>-</sup>. This property is vital for maintaining the probability interpretation in quantum mechanics.
-
Commutation Relations: The commutation relations involving these operators are:
[J<sub>z</sub>, J<sup>+</sup>] = ħJ<sup>+</sup> [J<sub>z</sub>, J<sup>-</sup>] = -ħJ<sup>-</sup> [J<sup>+</sup>, J<sup>-</sup>] = 2ħJ<sub>z</sub> [J², J<sup>+</sup>] = [J², J<sup>-</sup>] = 0
-
Normalization and Termination: The square root factors in their action on eigenstates guarantee proper normalization and ensure that the ladder operation terminates at the maximum and minimum values of m (m = j and m = -j, respectively). Attempting to raise beyond m = j or lower beyond m = -j results in zero.
-
Applications: Raising and lowering operators are essential in many quantum mechanical calculations. They simplify the computation of matrix elements, provide a systematic approach to constructing angular momentum eigenstates, and play a crucial role in the understanding of selection rules in spectroscopy and atomic physics.
Applications and Examples
The utility of raising and lowering operators extends to various areas:
1. Determining Matrix Elements:
Calculating matrix elements of angular momentum operators often involves complex calculations. The raising and lowering operators simplify this by providing a straightforward method to compute these elements. For example, the expectation value of J<sub>x</sub> and J<sub>y</sub> can be easily calculated using these operators.
2. Construction of Angular Momentum Eigenstates:
Starting with a known eigenstate (e.g., |j, j⟩), repeated application of the lowering operator J<sup>-</sup> generates all other eigenstates |j, m⟩ with m = j -1, j-2,..., -j. This provides a systematic way to construct the complete set of eigenstates for a given j.
3. Selection Rules in Spectroscopy:
In atomic spectroscopy, selection rules dictate which transitions between energy levels are allowed. These rules often involve the angular momentum of the involved states. Raising and lowering operators play a key role in deriving and understanding these selection rules, determining the allowed transitions based on the changes in angular momentum quantum numbers.
4. Spin Angular Momentum:
The concept of raising and lowering operators extends to spin angular momentum, denoted by S. Similar operators, S<sup>+</sup> and S<sup>-</sup>, can be defined, and their action on spin eigenstates follows the same principles as for orbital angular momentum. This is particularly important in understanding the behavior of electrons and other particles with intrinsic spin.
5. Isospin and Other Symmetries:
The mathematical formalism of angular momentum and its associated raising and lowering operators is not limited to the physical angular momentum of particles. These concepts find applications in other areas of physics, such as isospin symmetry in nuclear physics, where the operators act on isospin states rather than angular momentum states. This highlights the power and generality of the mathematical framework.
Beyond the Basics: More Advanced Concepts
This section briefly touches upon more advanced aspects related to raising and lowering operators:
-
Tensor Operators: Raising and lowering operators are special cases of tensor operators, which are operators that transform in a specific way under rotations. The study of tensor operators provides a more general framework for analyzing angular momentum in quantum systems.
-
Wigner-Eckart Theorem: This theorem provides a powerful tool for calculating matrix elements of tensor operators, including raising and lowering operators, by separating the geometric aspects (related to angular momentum) from the dynamic aspects (related to the specific physical interaction).
-
Irreducible Representations: The mathematical representation of angular momentum utilizes group theory, specifically the theory of rotations and their irreducible representations. Understanding these representations provides a deeper understanding of the properties and relationships between angular momentum states and operators.
Conclusion
Raising and lowering operators are indispensable tools for understanding and manipulating angular momentum in quantum mechanics. Their properties and applications are far-reaching, extending from basic calculations of matrix elements and the construction of eigenstates to advanced concepts in group theory and tensor operators. Mastering these operators is essential for anyone seeking a deep understanding of the quantum world and its diverse phenomena. Their systematic approach and elegant mathematical framework simplify complex calculations and provide valuable insights into the fundamental principles governing angular momentum in quantum systems. Furthermore, the conceptual framework extends beyond angular momentum to other areas of physics, showcasing its broader importance and utility.
Latest Posts
Latest Posts
-
What Does Salt Do In Dna Extraction
Apr 02, 2025
-
Why Is Water Necessary For Life
Apr 02, 2025
-
The Process Of Independent Assortment Refers To
Apr 02, 2025
-
Is Table Salt Homogeneous Or Heterogeneous
Apr 02, 2025
-
What Part Of Bacteria Cell Helps It Move
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Raising And Lowering Operators Angular Momentum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
