Type I And Type Ii Errors Examples
Muz Play
Mar 29, 2025 · 6 min read
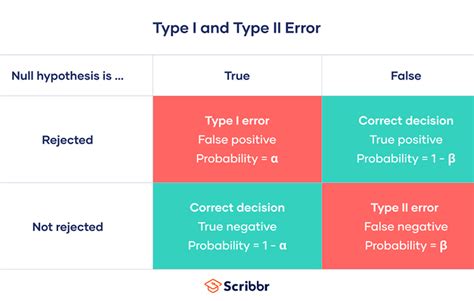
Table of Contents
Type I and Type II Errors: Examples and How to Minimize Them
Understanding Type I and Type II errors is crucial in various fields, from statistics and research to healthcare and business decision-making. These errors, also known as false positives and false negatives, represent the risk of drawing incorrect conclusions based on statistical analysis. This comprehensive guide will delve into the definitions, explore numerous examples across different domains, and provide practical strategies for minimizing the occurrence of these errors.
What are Type I and Type II Errors?
Before diving into examples, let's solidify our understanding of these two error types:
Type I Error (False Positive): A Type I error occurs when you reject the null hypothesis when it is actually true. In simpler terms, you conclude there's a significant effect or difference when, in reality, there isn't. The probability of committing a Type I error is denoted by alpha (α), often set at 0.05 (5%). This means there's a 5% chance of rejecting a true null hypothesis.
Type II Error (False Negative): A Type II error occurs when you fail to reject the null hypothesis when it is actually false. This means you conclude there's no significant effect or difference when, in reality, there is. The probability of committing a Type II error is denoted by beta (β). The power of a statistical test (1-β) represents the probability of correctly rejecting a false null hypothesis.
The Importance of Understanding Alpha and Beta
The relationship between alpha and beta is crucial. Lowering alpha (reducing the chance of a Type I error) often increases beta (increasing the chance of a Type II error), and vice versa. Finding the right balance depends heavily on the context and the consequences of each type of error.
For instance, in medical diagnosis, a Type I error (false positive – diagnosing a disease when it's not present) might lead to unnecessary treatment and anxiety, while a Type II error (false negative – failing to diagnose a disease when it's present) could have far more serious consequences.
Real-World Examples of Type I and Type II Errors
Let's explore numerous examples across various fields to illustrate these concepts:
Healthcare:
-
Type I Error: A patient tests positive for a rare disease (e.g., a specific type of cancer) through a screening test. However, further investigations (e.g., biopsy) reveal that the patient does not have the disease. The initial positive test resulted in unnecessary stress, anxiety, and possibly invasive procedures. The screening test had a high false positive rate.
-
Type II Error: A patient shows symptoms suggestive of a serious heart condition. However, an electrocardiogram (ECG) and other tests fail to detect the condition, leading to delayed treatment and potentially worsening health outcomes. The tests had a high false negative rate.
Criminal Justice:
-
Type I Error: An innocent person is convicted of a crime based on circumstantial evidence or flawed forensic analysis. This is a grave miscarriage of justice. The judicial process led to a false positive.
-
Type II Error: A guilty person is acquitted due to insufficient evidence or procedural errors. This allows a dangerous individual to remain free, potentially posing a threat to society. The judicial process resulted in a false negative.
Quality Control:
-
Type I Error: A batch of manufactured products is rejected due to a quality control test indicating a high defect rate. However, a subsequent, more thorough inspection shows that the defect rate is actually within acceptable limits. The initial test generated a false positive, leading to unnecessary waste and production delays.
-
Type II Error: A batch of manufactured products is accepted despite containing a significant number of defective items. This could lead to customer dissatisfaction, product recalls, and reputational damage. The initial test produced a false negative.
Scientific Research:
-
Type I Error: A researcher concludes that a new drug is effective based on a clinical trial, but further, larger-scale studies show no significant effect. The initial study produced a statistically significant result by chance (a false positive). Publication bias can exacerbate this issue.
-
Type II Error: A researcher fails to find a significant effect of a new treatment in a clinical trial, even though the treatment actually has a small but real effect. The study lacked sufficient power (high beta) to detect the effect (a false negative). This can lead to abandoning potentially beneficial treatments.
Marketing and Advertising:
-
Type I Error: A marketing campaign is deemed successful based on preliminary data showing a significant increase in sales. However, further analysis reveals that the increase was due to external factors (e.g., seasonal trends) rather than the campaign itself. The initial conclusion was a false positive.
-
Type II Error: A marketing campaign is deemed unsuccessful based on initial data showing no significant impact on sales. However, a more in-depth analysis reveals a slow but steady increase in brand awareness and customer loyalty that will translate into future sales. The initial conclusion was a false negative.
Minimizing Type I and Type II Errors
Several strategies can help minimize the risk of Type I and Type II errors:
-
Increase sample size: Larger sample sizes provide more statistical power, reducing the chance of Type II errors.
-
Improve the quality of data: Accurate and reliable data are essential for valid conclusions. This includes using appropriate measurement techniques and minimizing measurement error.
-
Use appropriate statistical tests: Selecting the correct statistical test for your data and research question is critical.
-
Adjust alpha level: While a 0.05 alpha level is common, it can be adjusted based on the context and the relative costs of Type I and Type II errors. A lower alpha level (e.g., 0.01) reduces the risk of Type I errors but increases the risk of Type II errors.
-
Increase the power of the test: Power (1-β) is the probability of correctly rejecting a false null hypothesis. Strategies to increase power include increasing the sample size and using more sensitive measurement tools.
-
Consider effect size: Focusing solely on statistical significance can be misleading. Consider the magnitude of the effect, even if it doesn't reach statistical significance. A small effect might still be practically meaningful.
-
Replicate studies: Repeating studies helps confirm the findings and reduce the influence of random error.
-
Use meta-analysis: Combining results from multiple studies provides a more robust estimate of the effect size and reduces the chance of drawing incorrect conclusions based on a single study.
Conclusion
Understanding and minimizing Type I and Type II errors is essential for making sound judgments based on data. By carefully considering the context, choosing appropriate statistical methods, and employing strategies to enhance the power and accuracy of research, we can significantly reduce the risk of drawing erroneous conclusions with potentially serious consequences. The examples provided highlight the real-world implications of these errors across diverse fields, underscoring the importance of a thorough understanding of this fundamental statistical concept. Continuous learning and critical evaluation of data analysis are crucial for reliable decision-making in any field that relies on statistical evidence.
Latest Posts
Latest Posts
-
Is Urea The Same As Uric Acid
Mar 31, 2025
-
How To Determine The Highest Boiling Point
Mar 31, 2025
-
How To Explain 10x In Lab Math
Mar 31, 2025
-
How To Make A Normal Probability Plot
Mar 31, 2025
-
Introspection Refers To A Process By Which Someone Examines
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Type I And Type Ii Errors Examples . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
