Using Hess's Law To Calculate Net Reaction Enthalpy
Muz Play
Mar 26, 2025 · 6 min read
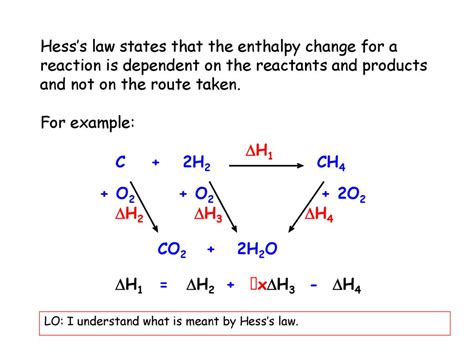
Table of Contents
Using Hess's Law to Calculate Net Reaction Enthalpy
Hess's Law, a cornerstone of thermochemistry, provides a powerful tool for calculating the enthalpy change (ΔH) of a reaction without directly measuring it experimentally. This law states that the total enthalpy change for a reaction is independent of the pathway taken. In simpler terms, the overall enthalpy change for a reaction is the same whether it occurs in one step or multiple steps. This principle allows us to determine the enthalpy change for reactions that are difficult or impossible to measure directly. This article will delve deep into the application of Hess's Law, exploring its theoretical basis, practical applications, and potential challenges.
Understanding Enthalpy and Hess's Law
Before diving into the calculations, let's establish a solid understanding of enthalpy. Enthalpy (H) is a thermodynamic property representing the total heat content of a system at constant pressure. The change in enthalpy (ΔH) during a reaction is the heat absorbed or released at constant pressure. A positive ΔH indicates an endothermic reaction (heat is absorbed), while a negative ΔH signifies an exothermic reaction (heat is released).
Hess's Law, mathematically, can be expressed as:
ΔH<sub>net</sub> = Σ ΔH<sub>products</sub> - Σ ΔH<sub>reactants</sub>
Where:
- ΔH<sub>net</sub> is the net enthalpy change of the reaction.
- Σ ΔH<sub>products</sub> is the sum of the enthalpies of formation of the products.
- Σ ΔH<sub>reactants</sub> is the sum of the enthalpies of formation of the reactants.
This equation emphasizes the importance of considering the stoichiometric coefficients of each species involved in the reaction. Each enthalpy of formation must be multiplied by its respective coefficient before summation.
Applying Hess's Law: A Step-by-Step Guide
Let's illustrate the application of Hess's Law with a detailed example. Suppose we want to determine the enthalpy change for the reaction:
C(s) + ½O<sub>2</sub>(g) → CO(g)
This reaction is difficult to measure directly with high accuracy. However, we know the enthalpy changes for the following reactions:
- C(s) + O<sub>2</sub>(g) → CO<sub>2</sub>(g) ΔH<sub>1</sub> = -393.5 kJ/mol
- CO(g) + ½O<sub>2</sub>(g) → CO<sub>2</sub>(g) ΔH<sub>2</sub> = -283.0 kJ/mol
We can use these known reactions to derive the desired reaction using Hess's Law. The process involves manipulating the given reactions algebraically to match the target reaction.
Step 1: Manipulating the Equations
Notice that in reaction 1, carbon (C) reacts with oxygen to form carbon dioxide (CO2). Reaction 2 shows carbon monoxide (CO) reacting with oxygen to form carbon dioxide. To get our target reaction, we need to combine these equations in a way that eliminates the unwanted species (CO2 in this case) and leaves only the reactants and products we need.
We can reverse reaction 2 to obtain:
- CO<sub>2</sub>(g) → CO(g) + ½O<sub>2</sub>(g) ΔH<sub>3</sub> = +283.0 kJ/mol (Note the sign change!)
Step 2: Combining the Equations
Now, we add reaction 1 and reaction 3:
C(s) + O<sub>2</sub>(g) → CO<sub>2</sub>(g) CO<sub>2</sub>(g) → CO(g) + ½O<sub>2</sub>(g)
C(s) + ½O<sub>2</sub>(g) → CO(g)
Observe that CO<sub>2</sub> cancels out, leaving us with our target reaction.
Step 3: Calculating the Net Enthalpy Change
The net enthalpy change (ΔH<sub>net</sub>) is the sum of the enthalpy changes of the manipulated reactions:
ΔH<sub>net</sub> = ΔH<sub>1</sub> + ΔH<sub>3</sub> = -393.5 kJ/mol + 283.0 kJ/mol = -110.5 kJ/mol
Therefore, the enthalpy change for the reaction C(s) + ½O<sub>2</sub>(g) → CO(g) is -110.5 kJ/mol. This signifies an exothermic reaction.
Advanced Applications and Considerations
While the above example illustrates a straightforward application, Hess's Law can handle more complex scenarios involving multiple intermediate steps. The key is to systematically manipulate the given equations through addition, subtraction, and multiplication (with corresponding enthalpy adjustments) to obtain the desired target reaction.
Dealing with Fractional Coefficients
Often, you'll encounter reactions with fractional stoichiometric coefficients. Remember that these coefficients affect the enthalpy change. If you multiply a reaction by a factor, you must multiply its enthalpy change by the same factor. This is because enthalpy is an extensive property—it depends on the amount of substance.
Standard Enthalpies of Formation
For most calculations, standard enthalpies of formation (ΔH<sub>f</sub>°) are used. These are enthalpy changes when one mole of a compound is formed from its constituent elements in their standard states (usually at 298 K and 1 atm pressure). Using standard enthalpies ensures consistency and simplifies the calculation. Extensive tables of standard enthalpies of formation are available in chemistry handbooks and online databases.
Limitations of Hess's Law
Although a powerful tool, Hess's Law has limitations. It relies on the availability of enthalpy data for the relevant reactions. If such data is lacking, the law cannot be applied. Additionally, the accuracy of the calculated enthalpy change is dependent on the accuracy of the individual enthalpy values used in the calculation. Any uncertainties in the individual enthalpy values will propagate to the final result.
Practical Applications of Hess's Law
Hess's Law finds widespread use in various fields:
- Thermochemistry: Predicting the enthalpy changes for reactions that are difficult or impossible to measure directly. This is crucial in understanding reaction spontaneity and energy balances.
- Chemical Engineering: Designing and optimizing chemical processes by predicting energy requirements and optimizing reaction pathways.
- Materials Science: Studying the thermodynamics of material formation and transformations, crucial for designing new materials with desired properties.
- Environmental Science: Assessing the energy changes associated with environmental processes, such as combustion and decomposition reactions.
Troubleshooting Common Mistakes
Students often encounter several common pitfalls when applying Hess's Law:
- Incorrectly manipulating equations: Failing to change the sign of ΔH when reversing a reaction or forgetting to multiply ΔH when multiplying the stoichiometric coefficients.
- Ignoring stoichiometric coefficients: Not multiplying the enthalpy changes by the appropriate stoichiometric coefficients before summing.
- Incorrectly identifying intermediate species: Not correctly identifying and canceling out intermediate species in the combined reactions.
- Misinterpreting enthalpy signs: Confusing exothermic and endothermic reactions based on the sign of ΔH.
Conclusion
Hess's Law is a fundamental principle in thermochemistry offering a valuable method for determining reaction enthalpy changes. By manipulating known enthalpy changes of reactions, we can calculate the enthalpy change for a reaction that may be experimentally difficult or impossible to measure directly. Understanding the principles and carefully applying the stepwise procedure outlined above will empower you to accurately and efficiently calculate net reaction enthalpies and leverage this powerful tool in various scientific disciplines. Mastering Hess's Law enhances problem-solving skills and deepens the understanding of thermodynamic principles underpinning chemical reactions. Always remember to double-check your calculations, paying close attention to signs and stoichiometric coefficients to ensure accuracy.
Latest Posts
Latest Posts
-
Write The Relation As A Set Of Ordered Pairs
Mar 29, 2025
-
Us History Reconstruction To The Present
Mar 29, 2025
-
Label The Structures Of The Upper Respiratory System
Mar 29, 2025
-
Assigning R And S Configuration Practice
Mar 29, 2025
-
Does Higher Pka Mean Stronger Acid
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Using Hess's Law To Calculate Net Reaction Enthalpy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
