Van Der Waals Equation A And B Values
Muz Play
Apr 07, 2025 · 6 min read
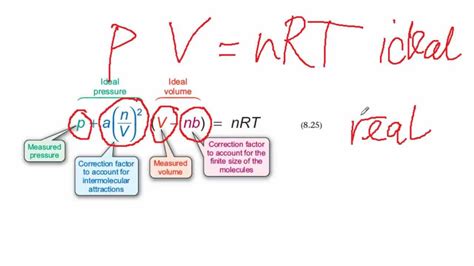
Table of Contents
Understanding van der Waals Equation: A Deep Dive into 'a' and 'b' Values
The ideal gas law, while a useful simplification, fails to accurately describe the behavior of real gases, especially at high pressures and low temperatures. This is because it neglects intermolecular forces and the finite volume occupied by gas molecules. Johannes Diderik van der Waals addressed these shortcomings by introducing a modified equation of state, now famously known as the van der Waals equation. This equation incorporates two crucial parameters, 'a' and 'b', which account for the attractive forces and the finite volume of gas molecules, respectively. Understanding these parameters is key to appreciating the power and limitations of the van der Waals equation.
The van der Waals Equation: A Recap
The van der Waals equation is expressed as:
(P + a(n/V)²)(V - nb) = nRT
Where:
- P represents the pressure of the gas.
- V represents the volume of the gas.
- n represents the number of moles of the gas.
- R represents the ideal gas constant.
- T represents the temperature of the gas.
- a is a correction factor that accounts for the attractive intermolecular forces between gas molecules.
- b is a correction factor that accounts for the finite volume occupied by gas molecules.
Deconstructing the 'a' Parameter: The Intermolecular Attraction Factor
The 'a' parameter quantifies the strength of the attractive forces between gas molecules. These forces, predominantly van der Waals forces (including London dispersion forces, dipole-dipole interactions, and hydrogen bonding), cause deviations from ideal gas behavior. Stronger attractive forces lead to a larger 'a' value.
Influence of Molecular Structure on 'a'
The magnitude of 'a' is highly dependent on the molecular structure of the gas. Larger, more complex molecules with greater surface area tend to exhibit stronger intermolecular forces and thus possess larger 'a' values. This is because larger molecules have more electrons, leading to stronger London dispersion forces. Polar molecules, with their permanent dipoles, experience stronger dipole-dipole interactions, further increasing the 'a' value. Molecules capable of hydrogen bonding exhibit exceptionally strong attractive forces, resulting in significantly larger 'a' values compared to non-polar molecules of similar size.
Impact of 'a' on Gas Behavior
A larger 'a' value implies stronger attractive forces, leading to:
- Lower observed pressures: The attractive forces pull the molecules closer together, reducing the impact of their collisions on the container walls, resulting in a lower measured pressure than predicted by the ideal gas law.
- Increased liquefaction tendency: Stronger attractive forces make it easier for the gas to transition to the liquid phase, as the molecules are more readily attracted to each other. This is reflected in a lower critical temperature and a higher critical pressure.
Decoding the 'b' Parameter: The Co-volume Factor
The 'b' parameter accounts for the finite volume occupied by the gas molecules themselves. The ideal gas law assumes that gas molecules are point masses with negligible volume, an assumption that breaks down at high pressures where the volume of the molecules becomes a significant fraction of the total volume. The 'b' value represents the volume excluded from the total volume V due to the finite size of the molecules. It is essentially the co-volume, representing the space inaccessible to other molecules due to the presence of a given molecule.
Relationship between 'b' and Molecular Size
The 'b' value is directly related to the size of the gas molecules. Larger molecules have larger 'b' values as they occupy a greater volume. This makes intuitive sense; a larger molecule will exclude a larger volume for other molecules to occupy.
The Role of 'b' in Gas Behavior
A larger 'b' value implies larger molecules and a greater excluded volume, leading to:
- Higher observed pressures: Because the molecules occupy a significant portion of the container's volume, the effective volume available for the molecules to move around in is reduced. This leads to more frequent collisions with the container walls, resulting in a higher pressure than predicted by the ideal gas law.
- Reduced compressibility: The finite volume of the molecules makes the gas less compressible than an ideal gas, as there is less empty space for the molecules to be compressed into.
Determining 'a' and 'b' Values: Experimental and Theoretical Approaches
The 'a' and 'b' values are specific to each gas and are determined either experimentally or through theoretical calculations based on intermolecular potential models.
Experimental Determination
Experimentally, 'a' and 'b' values can be determined by fitting the van der Waals equation to experimentally measured pressure-volume-temperature (PVT) data. This typically involves sophisticated regression analysis techniques to find the best fit values for 'a' and 'b' that minimize the deviation between the experimental data and the predictions of the van der Waals equation.
Theoretical Estimation
Theoretical estimations of 'a' and 'b' often rely on intermolecular potential models, which provide a mathematical description of the forces between gas molecules. These models can then be used to calculate the attractive forces and the excluded volume, allowing for the estimation of 'a' and 'b' values. However, the accuracy of these theoretical estimates heavily depends on the sophistication of the intermolecular potential model used.
Limitations of the van der Waals Equation
While a significant improvement over the ideal gas law, the van der Waals equation is still an approximation. It does not perfectly capture the behavior of real gases under all conditions. Its limitations include:
- Simplicity of the model: The van der Waals equation uses simplified assumptions about the nature of intermolecular forces and molecular volume. Real intermolecular forces are far more complex, and the actual shape and size of molecules are not perfectly represented by a simple 'b' parameter.
- Inaccuracy at very high pressures and low temperatures: The equation performs poorly under conditions where the gas is close to its critical point or below its critical temperature, where the gas can undergo phase transitions. More complex equations of state are needed to accurately model gas behavior under these conditions.
- Temperature dependence of 'a' and 'b': The van der Waals equation assumes constant values of 'a' and 'b', regardless of temperature. In reality, both parameters exhibit some degree of temperature dependence, which is not captured in the equation.
Applications and Significance of the van der Waals Equation
Despite its limitations, the van der Waals equation remains a valuable tool in several applications:
- Estimation of gas properties: It provides reasonable estimations of gas properties such as pressure, volume, and temperature under conditions where the ideal gas law is inadequate.
- Understanding phase transitions: It offers insights into the behavior of gases near their critical point and helps explain the conditions for liquefaction.
- Chemical engineering design: It plays a role in designing and optimizing chemical processes, especially those involving high-pressure gases.
- Educational tool: Its simplified representation of intermolecular forces and molecular volume helps students understand the complexities of real gas behavior.
Conclusion
The van der Waals equation, with its 'a' and 'b' parameters, stands as a landmark achievement in our understanding of real gases. While not a perfect representation of reality, its incorporation of intermolecular forces and finite molecular volume significantly improves upon the ideal gas law, providing a valuable tool for approximating real gas behavior in numerous applications. Further research and development continue to refine our understanding of intermolecular interactions and improve upon the van der Waals equation, leading to more accurate and sophisticated equations of state that better capture the complexities of real gas behavior. The enduring legacy of the van der Waals equation lies in its ability to bridge the gap between the idealized behavior of gases and the more intricate realities of the world around us.
Latest Posts
Latest Posts
-
An Atomic Nucleus Has A Mass That Is
Apr 09, 2025
-
Graph Atomic Radius Vs Atomic Number
Apr 09, 2025
-
How Many Valence Electrons Are In Be
Apr 09, 2025
-
Ground State Electron Configuration For Calcium
Apr 09, 2025
-
How Is Hydrate Different From Other Chemical Compounds
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Van Der Waals Equation A And B Values . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.