What Does The Nernst Equation Tell Us
Muz Play
Mar 30, 2025 · 5 min read
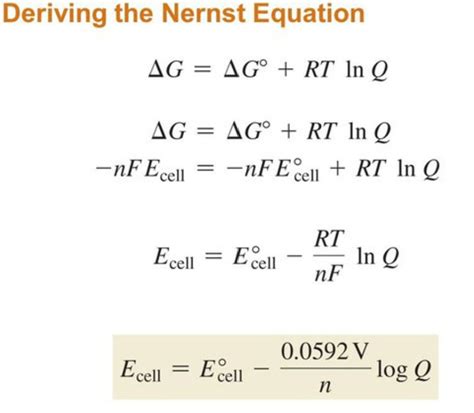
Table of Contents
What Does the Nernst Equation Tell Us? A Deep Dive into Electrochemical Potential
The Nernst equation is a cornerstone of electrochemistry, providing a crucial link between the thermodynamics of a redox reaction and its electrical potential. It allows us to calculate the cell potential under non-standard conditions, offering invaluable insights into electrochemical processes occurring in batteries, fuel cells, biological systems, and various industrial applications. This article will explore the Nernst equation in depth, explaining its derivation, applications, limitations, and its broader significance in understanding electrochemical behavior.
Understanding the Fundamentals: Standard Reduction Potential and Equilibrium
Before delving into the Nernst equation itself, it's vital to grasp the concepts of standard reduction potential and electrochemical equilibrium.
Standard Reduction Potential (E°)
The standard reduction potential (E°) represents the tendency of a chemical species to acquire electrons and be reduced under standard conditions (298 K, 1 atm pressure, 1 M concentration). Each redox half-reaction has its own associated standard reduction potential, tabulated in standard reduction potential tables. A more positive E° indicates a greater tendency to be reduced (stronger oxidizing agent), while a more negative E° signifies a greater tendency to be oxidized (stronger reducing agent).
Electrochemical Equilibrium
At equilibrium, the forward and reverse rates of a redox reaction are equal, resulting in no net change in concentrations or electrical potential. The equilibrium constant (K) quantifies the relative concentrations of reactants and products at equilibrium. A large K value signifies a reaction that strongly favors product formation, while a small K indicates a preference for reactants.
Deriving the Nernst Equation: Linking Potential, Concentration, and Equilibrium
The Nernst equation bridges the gap between the standard reduction potential (E°) and the actual cell potential (E) under non-standard conditions. It considers the influence of reactant and product concentrations on the overall cell potential. The derivation relies on the relationship between Gibbs Free Energy (ΔG), equilibrium constant (K), and cell potential (E):
ΔG = -nFE
where:
- ΔG is the change in Gibbs Free Energy
- n is the number of moles of electrons transferred in the balanced redox reaction
- F is Faraday's constant (96,485 C/mol)
- E is the cell potential
Under standard conditions, this becomes:
ΔG° = -nFE°
The relationship between ΔG and ΔG° is given by:
ΔG = ΔG° + RTlnQ
where:
- R is the ideal gas constant (8.314 J/mol·K)
- T is the temperature in Kelvin
- Q is the reaction quotient, representing the ratio of product concentrations to reactant concentrations at any given time (not necessarily equilibrium).
Substituting the expressions for ΔG and ΔG° into the equation above, and solving for E, we obtain the Nernst equation:
E = E° - (RT/nF)lnQ
This is the fundamental form of the Nernst equation. Often, it's expressed at 25°C (298 K) using base-10 logarithms:
E = E° - (0.0592/n)logQ
Applications of the Nernst Equation: Unlocking Electrochemical Mysteries
The Nernst equation finds extensive applications in various fields:
1. Predicting Cell Potential Under Non-Standard Conditions:
The most straightforward application is calculating the cell potential when the concentrations of reactants and products deviate from standard conditions. This is crucial for understanding the performance of batteries and fuel cells under varying operating conditions.
2. Determining Equilibrium Constants (K):
At equilibrium, Q = K, and E = 0. Therefore, the Nernst equation can be rearranged to calculate the equilibrium constant:
K = exp[(nFE°)/(RT)]
This allows us to determine the extent to which a redox reaction will proceed to completion.
3. Analyzing Electrochemical Sensors:
Many electrochemical sensors utilize the Nernst equation to relate the measured potential to the concentration of an analyte. The potential change is directly proportional to the logarithm of the analyte concentration.
4. Understanding Biological Systems:
The Nernst equation is critical in understanding the electrochemical gradients across cell membranes, which drive ion transport and various biological processes. The membrane potential, for example, can be calculated using a modified form of the Nernst equation that considers the permeabilities of different ions.
5. Corrosion Engineering:
The Nernst equation helps predict the corrosion rate of metals in various environments. The potential difference between the metal and its environment determines the driving force for corrosion.
Limitations and Considerations of the Nernst Equation
While the Nernst equation is a powerful tool, it has certain limitations:
- Ideal Behavior: It assumes ideal behavior of the solution, neglecting activities and non-idealities. At high concentrations, deviations from ideality become significant.
- Activity Coefficients: For more accurate calculations, activity coefficients should be incorporated to account for non-ideal behavior.
- Temperature Dependence: The equation is temperature-dependent, and the values of E° and Q are affected by temperature changes.
- Reaction Kinetics: The Nernst equation deals with equilibrium potentials. It doesn't directly address the kinetics of electron transfer, which can be crucial in determining the actual rate of a redox reaction.
- Complex Reactions: For complex reactions involving multiple steps and intermediate species, the application of the Nernst equation might become more challenging.
Beyond the Basics: Expanding Our Understanding
The Nernst equation provides a foundational understanding of electrochemical potential. However, a comprehensive understanding requires considering other factors:
- Electrode Kinetics: The rate of electron transfer at the electrode surface significantly impacts the observed potential. Electrode kinetics is governed by factors like overpotential and exchange current density.
- Mass Transport: The transport of reactants and products to and from the electrode surface can limit the reaction rate. Mass transport processes include diffusion, migration, and convection.
- Polarization: Deviations from the equilibrium potential due to the passage of current are called polarization. Different types of polarization (activation, concentration, and ohmic) can influence the cell performance.
Conclusion: The Nernst Equation's Enduring Importance
The Nernst equation, despite its limitations, remains a cornerstone of electrochemistry. It provides a quantitative link between thermodynamics and electrochemistry, enabling the prediction and interpretation of electrochemical behavior under various conditions. Its applications span numerous fields, from energy storage and conversion to biological systems and analytical chemistry. Understanding the Nernst equation is essential for anyone studying or working with electrochemical processes, providing a fundamental framework for understanding the complex interplay between electrical potential, concentration, and equilibrium. While it's crucial to be aware of its limitations, the Nernst equation serves as an invaluable tool for interpreting and predicting electrochemical phenomena. Its continued importance is underscored by its ongoing relevance in both fundamental research and practical applications. Further exploration into electrode kinetics, mass transport, and polarization effects allows for a more nuanced understanding of real-world electrochemical systems.
Latest Posts
Latest Posts
-
Root Mean Square Velocity Of Gas
Apr 01, 2025
-
Where Is The Respiratory Center Located In The Brain
Apr 01, 2025
-
What Is The Difference Between Cellular Respiration And Fermentation
Apr 01, 2025
-
What Are Two Functional Groups Found In Amino Acids
Apr 01, 2025
-
Foundations Of Education 13th Edition Pdf Free Download
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Does The Nernst Equation Tell Us . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
