Work Is The Integral Of Force
Muz Play
Mar 31, 2025 · 7 min read
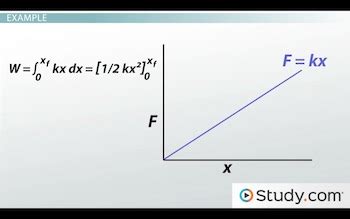
Table of Contents
Work is the Integral of Force: A Deep Dive into Physics and Engineering
The deceptively simple statement, "work is the integral of force," underpins a vast swathe of physics and engineering. It's a concept that governs everything from designing bridges and launching rockets to understanding the motion of planets and the behavior of atoms. This article will delve into this fundamental principle, exploring its mathematical formulation, its various applications, and the nuanced understanding required to master its implications.
Understanding Work: Beyond the Everyday Meaning
In everyday conversation, "work" often implies exertion of effort. While related, the physics definition is far more precise. In physics, work is done when a force causes a displacement of an object. Crucially, the force must have a component acting in the direction of the displacement. Simply pushing against an immovable wall, however strenuous, performs no work in the physics sense because there is no displacement.
This key distinction leads us to the mathematical representation:
Work (W) = ∫ F ⋅ ds
Where:
- W represents work, typically measured in Joules (J).
- ∫ denotes the integral, signifying the summation of infinitesimal contributions.
- F is the force vector, encompassing both magnitude and direction.
- ds is an infinitesimal displacement vector along the path of the object.
- ⋅ represents the dot product, which considers only the component of the force parallel to the displacement.
This equation encapsulates the core principle: work is the accumulation of the force's effect over the entire distance the object moves. If the force is constant and acts in the same direction as the displacement, the integral simplifies to:
W = Fd
Where:
- F is the constant force.
- d is the displacement.
However, this simplified equation is only applicable in specific scenarios. In most real-world situations, the force varies in magnitude or direction along the path, necessitating the use of the integral form.
The Integral's Significance: Accounting for Variable Forces
The integral's importance lies in its ability to handle situations where the force isn't constant. Consider a spring: the force it exerts is proportional to its extension (Hooke's Law: F = -kx, where k is the spring constant and x is the extension). To calculate the work done in stretching the spring from its relaxed state to a length x, we must integrate:
W = ∫₀ˣ kx dx = ½kx²
This shows the work done is proportional to the square of the extension. The integral correctly captures the fact that the force is progressively increasing as the spring is stretched.
Similarly, consider lifting an object in a gravitational field. While the gravitational force (weight) is approximately constant near the Earth's surface, if we lift the object to a significant height, the force will vary slightly due to changes in the gravitational field. The integral would be needed for precise calculation in this scenario.
Furthermore, the integral allows for the consideration of curved paths. If a force acts on an object moving along a curved trajectory, the integral accounts for the continuously changing direction of both the force and the displacement vector. This is crucial in scenarios like a satellite orbiting the Earth or a rollercoaster traversing its track.
Applications Across Diverse Fields
The concept of "work is the integral of force" is fundamental across a multitude of scientific and engineering disciplines. Let's examine some key applications:
1. Mechanical Engineering:
- Machine Design: Engineers utilize this principle to design machines that efficiently perform work. Understanding the forces involved and their variations is critical for optimizing machine performance and minimizing energy waste. This principle directly relates to calculating power output, efficiency, and determining appropriate motor selection.
- Structural Analysis: Calculating the work done by external loads on a structure is essential for determining its stability and strength. The integral approach accurately models the stresses and strains within the structure under different load conditions, ensuring its structural integrity.
- Robotics: Robot locomotion and manipulation involve calculating the work done by actuators to move the robot and objects. The precise calculation of forces and their integration are essential for accurate control and efficient energy usage.
2. Electrical Engineering:
- Circuit Analysis: While seemingly unrelated, the concept of work finds application in electrical circuits. The work done in moving a charge through a potential difference is defined as the voltage multiplied by the charge. For complex circuits, integration techniques can be used to accurately calculate energy dissipation or energy storage.
- Electromagnetism: The work done on a charged particle moving in an electromagnetic field can be expressed as an integral involving the Lorentz force.
3. Aerospace Engineering:
- Rocket Propulsion: Calculating the work done by rocket engines involves integrating the thrust force over the duration of the burn. This is essential for determining the change in velocity and the altitude attained by the rocket. The varying thrust during different stages of flight mandates the use of the integral approach for precise analysis.
- Orbital Mechanics: Understanding the work done by gravitational forces on satellites and spacecraft is critical for trajectory planning and mission design. The integral form accounts for the varying gravitational pull at different altitudes and positions.
4. Civil Engineering:
- Bridge Design: The integral of force is crucial in determining the stresses and strains within a bridge structure under various load conditions. This involves integrating the force of traffic, wind, and the bridge's own weight to ensure stability and safety.
- Dam Design: The integral approach is vital for assessing the pressure exerted by water against a dam. The pressure varies with depth, necessitating integration to calculate the total force and subsequently the work needed to overcome it.
5. Physics:
- Classical Mechanics: The principle forms the backbone of many calculations in classical mechanics, from simple projectile motion to complex interactions between multiple bodies.
- Thermodynamics: Work plays a central role in thermodynamics, particularly in the context of various thermodynamic processes. For instance, the work done during an isothermal expansion of a gas is calculated using integration.
- Quantum Mechanics: While seeming distant from the classical notion, the integral formulation of work finds subtle parallels in quantum mechanics calculations, particularly when considering potential energy and the wave function.
Beyond the Basics: Conservative and Non-Conservative Forces
The concept of work further branches into important distinctions between conservative and non-conservative forces.
Conservative forces are those for which the work done is independent of the path taken. Gravity is an excellent example: the work done in lifting an object from point A to point B is the same regardless of the route taken. For conservative forces, the work done can be expressed as the negative change in potential energy:
W = -ΔU
Non-conservative forces, such as friction, depend on the path taken. The work done against friction in sliding an object across a surface will be greater if the path is longer. For non-conservative forces, the work done cannot be expressed simply as a change in potential energy. The path dependency makes the integral calculation crucial for accurate results.
Practical Considerations and Numerical Methods
While the integral provides the theoretical framework, practical application often requires numerical methods. For complex scenarios with intricate force variations or irregular paths, analytical integration might be impossible or exceedingly difficult. Numerical techniques, such as the trapezoidal rule or Simpson's rule, offer effective approximations to the integral, allowing for accurate calculations in practical engineering problems. Software packages utilizing these numerical methods are indispensable tools in various engineering disciplines.
Conclusion: A Cornerstone of Physics and Engineering
"Work is the integral of force" is more than just a mathematical equation; it's a fundamental principle shaping our understanding of the physical world. Its application extends far beyond introductory physics textbooks, underpinning the design and analysis of complex systems across numerous engineering fields. Understanding the nuances of this principle – the integral's significance, the distinction between conservative and non-conservative forces, and the need for numerical methods – is essential for anyone striving for a deeper grasp of physics and its real-world applications. The continuous interplay between theoretical understanding and practical implementation through numerical techniques solidifies its position as a cornerstone of modern engineering and scientific progress.
Latest Posts
Latest Posts
-
Is Table Salt Homogeneous Or Heterogeneous
Apr 02, 2025
-
What Part Of Bacteria Cell Helps It Move
Apr 02, 2025
-
Is The Organic Layer On The Top Or Bottom
Apr 02, 2025
-
In A Solution It Is Dissolving Medium
Apr 02, 2025
-
How To Find Moles Of Naoh Used In Titration
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Work Is The Integral Of Force . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
