Center Of Pressure In Fluid Mechanics
Muz Play
Mar 29, 2025 · 6 min read
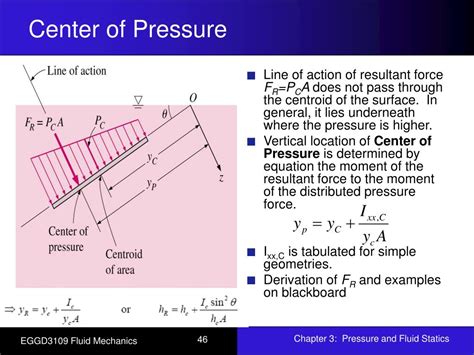
Table of Contents
Center of Pressure: A Deep Dive into Fluid Mechanics
The concept of the center of pressure (CP) is fundamental in fluid mechanics, particularly crucial in understanding how fluids exert forces on submerged or immersed bodies. This comprehensive guide delves into the intricacies of CP, explaining its definition, calculation methods, applications, and implications across various engineering disciplines. We’ll explore its significance in diverse scenarios, from the design of airplanes and ships to the stability of dams and offshore structures.
Defining the Center of Pressure
The center of pressure is the single point on a submerged surface where the total hydrodynamic force acting on that surface can be considered to act. Imagine a flat plate submerged in a fluid; the pressure exerted by the fluid isn't uniform across the entire surface. The pressure increases with depth, resulting in a larger force at greater depths. The center of pressure represents the point through which the resultant of all these distributed pressure forces acts. It's crucial to understand that the CP is not necessarily located at the centroid (geometric center) of the submerged surface. This distinction is critical in accurate force analysis.
Distinguishing CP from Centroid
The centroid represents the geometric center of a shape, a purely geometric property. In contrast, the center of pressure is a hydrodynamic property, dependent on the fluid pressure distribution. While they may coincide in specific cases (e.g., a horizontally submerged rectangular plate), they generally differ, especially for irregularly shaped bodies or surfaces at inclined angles to the fluid surface. This difference arises because the pressure distribution is non-uniform, causing the resultant force to act at a point offset from the centroid.
Calculating the Center of Pressure: Methods and Approaches
Calculating the center of pressure necessitates understanding the pressure distribution on the submerged surface. This often involves integrating pressure over the surface area. Two common methods are prevalent:
1. Integration Method
This rigorous method involves directly integrating the pressure distribution over the submerged area. The following steps outline the process:
-
Define the coordinate system: Establish a suitable Cartesian coordinate system with its origin at a convenient point (often at the fluid surface).
-
Determine the pressure distribution: Express the pressure (P) at any point on the surface as a function of its coordinates (x, y). This typically involves applying hydrostatic pressure principles: P = ρgh, where ρ is the fluid density, g is the acceleration due to gravity, and h is the depth of the point below the free surface.
-
Calculate the resultant force: Integrate the pressure over the submerged surface to find the total force (F): F = ∫∫ P dA, where dA is a differential area element.
-
Calculate the moments: Determine the moments of the pressure forces about the chosen coordinate axes. For example, the moment about the x-axis (Mx) is: Mx = ∫∫ x * P dA. Similarly, calculate the moment about the y-axis (My).
-
Determine the center of pressure coordinates: The coordinates of the center of pressure (xcp, ycp) are then given by:
xcp = Mx / F ycp = My / F
This method requires proficiency in calculus and integral techniques, but it provides an accurate representation of the center of pressure. It's particularly valuable for complex surface geometries.
2. Simplified Approach for Simple Geometries
For simpler geometries like rectangular or triangular plates, simplified formulations can be used. These formulas are derived from the integration method but offer a more straightforward calculation. These simplified equations often provide accurate results for regularly shaped bodies in specific orientations. They are extensively used in introductory fluid mechanics courses and engineering practice.
Example: Rectangular Plate
For a rectangular plate submerged vertically with its top edge at depth h1 and bottom edge at depth h2, the depth of the center of pressure (hcp) is given by:
hcp = (h1 + h2)/2 + (I_g / (A * (h2-h1)))
where:
- I_g is the second moment of area of the rectangle about its centroidal axis.
- A is the area of the rectangle.
This equation illustrates how the center of pressure deviates from the centroid. The term (I_g / (A * (h2-h1))) represents the shift in the CP's location due to the non-uniform pressure distribution.
Applications of Center of Pressure
The concept of the center of pressure finds extensive applications across multiple engineering disciplines:
1. Aerospace Engineering: Aircraft Stability and Control
In aircraft design, understanding the center of pressure of the wings and control surfaces (ailerons, elevators, rudders) is critical for stability and control. The location of the center of pressure relative to the center of gravity influences the aircraft's pitch, roll, and yaw stability. An improperly positioned CP can lead to instability and potentially catastrophic consequences.
2. Naval Architecture: Ship Stability and Buoyancy
In naval architecture, the center of pressure on the hull is essential for analyzing ship stability. The interaction between the center of pressure of buoyant forces and the ship's center of gravity determines the vessel's ability to remain upright in various sea states. Understanding the CP is crucial in preventing capsizing.
3. Civil Engineering: Dam Stability and Design
The pressure exerted by water on a dam's face creates a resultant force whose point of application is the center of pressure. Accurate determination of this CP is paramount in dam design to ensure structural integrity and prevent failure. The design must account for the varying water levels and pressure distributions to ensure stability.
4. Offshore Engineering: Platform Stability and Design
Offshore structures, like oil platforms and wind turbines, are subjected to significant hydrodynamic forces from waves and currents. Precise calculations of the center of pressure are vital in ensuring their structural stability and resistance to environmental loads. Improper CP consideration can lead to structural fatigue and eventual collapse.
5. Submarine Design and Operation
Submarines experience significant pressure changes at different depths. Understanding the CP on the hull and other submerged surfaces allows engineers to design pressure hulls that can withstand the immense forces encountered at varying depths.
6. Hydrodynamic Bearings
In machinery and fluid power systems, hydrodynamic bearings utilize the pressure generated by fluid film to support rotating shafts. The center of pressure plays a key role in determining the bearing's load capacity, stability, and efficiency.
Factors Affecting the Center of Pressure
Several factors influence the location of the center of pressure:
-
Shape of the submerged body: Irregular shapes lead to complex pressure distributions and potentially significant deviations of the CP from the centroid.
-
Orientation of the body: The angle of the submerged surface relative to the fluid surface greatly affects the pressure distribution and, therefore, the CP location.
-
Fluid density: A higher fluid density results in higher pressures and, potentially, a different CP location.
-
Fluid velocity: While less dominant in static situations, fluid velocity influences pressure distribution through dynamic pressure effects (Bernoulli's principle).
Conclusion
The center of pressure is a fundamental concept with significant practical implications in a variety of engineering disciplines. Accurate determination of the CP requires careful consideration of pressure distribution and often involves complex mathematical calculations. Understanding this concept is paramount for engineers and designers aiming to create safe, stable, and efficient structures and systems operating in fluid environments. From the stability of airplanes and ships to the integrity of dams and offshore platforms, the proper understanding and application of the center of pressure principles are critical for ensuring structural safety and functional effectiveness. The methods described in this article provide a framework for determining the center of pressure for various geometries and scenarios, underscoring the crucial role of fluid mechanics in numerous engineering applications.
Latest Posts
Latest Posts
-
Modeling How Dna Fingerprints Are Made
Apr 01, 2025
-
Where Is Genetic Information Of The Cell Stored
Apr 01, 2025
-
The Amount Of Matter In An Object Is
Apr 01, 2025
-
What Is The Amdr For Fat For Adults
Apr 01, 2025
-
What Is The Difference Between A Closed And Open System
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Center Of Pressure In Fluid Mechanics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
