Does Sohcahtoa Work On Non Right Triangles
Muz Play
Apr 03, 2025 · 5 min read
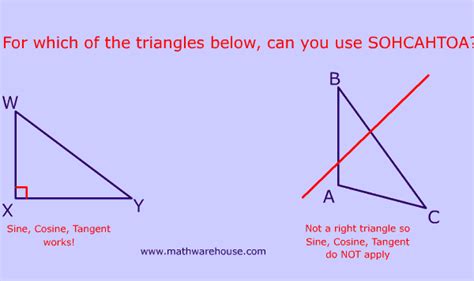
Table of Contents
Does SOHCAHTOA Work on Non-Right Triangles?
SOHCAHTOA, the mnemonic for the trigonometric ratios (Sine, Cosine, Tangent), is a cornerstone of trigonometry. It's drilled into students as the fundamental way to solve for unknown sides and angles in right-angled triangles. But what happens when we encounter triangles that aren't right-angled? Does SOHCAHTOA still hold true? The short answer is: no, directly applying SOHCAHTOA to non-right triangles is incorrect. However, the underlying principles of sine, cosine, and tangent remain relevant and are extended through other powerful trigonometric laws. This article will delve deep into why SOHCAHTOA fails for non-right triangles and explain the appropriate methods to tackle these problems.
Understanding SOHCAHTOA and its Limitations
Before exploring alternatives, let's reinforce the meaning of SOHCAHTOA:
- SOH: Sine = Opposite/Hypotenuse
- CAH: Cosine = Adjacent/Hypotenuse
- TOA: Tangent = Opposite/Adjacent
The key element here is the hypotenuse, which is only defined for right-angled triangles – it's the side opposite the right angle. Non-right triangles, by definition, lack this specific side. Trying to directly apply these ratios to a non-right triangle would lead to incorrect calculations because the concept of "opposite" and "adjacent" become ambiguous without a clearly defined right angle.
The Sine Rule and Cosine Rule: Extensions for Non-Right Triangles
Fortunately, trigonometry provides more general laws that transcend the limitations of SOHCAHTOA: the Sine Rule and the Cosine Rule. These are powerful tools for solving non-right triangles.
The Sine Rule
The Sine Rule establishes a relationship between the sides and angles of any triangle:
a/sin A = b/sin B = c/sin C
where:
- a, b, c are the lengths of the sides opposite angles A, B, C respectively.
This rule is particularly useful when you know:
- Two angles and one side (AAS or ASA): You can use the Sine Rule to find the remaining sides.
- Two sides and an angle opposite one of them (SSA): This case can be ambiguous, meaning there might be two possible triangles that satisfy the given conditions. Careful consideration is required.
Example: Imagine a triangle with angles A = 40°, B = 60°, and side a = 5cm. Using the Sine Rule, we can find side b:
5/sin 40° = b/sin 60°
b = 5 * sin 60° / sin 40° ≈ 6.78 cm
The Cosine Rule
The Cosine Rule provides another relationship between sides and angles, offering a different approach to solving non-right triangles:
a² = b² + c² - 2bc * cos A
(Similar formulas can be written for b² and c²)
The Cosine Rule is invaluable when you know:
- Three sides (SSS): You can use it to find any of the angles.
- Two sides and the included angle (SAS): You can use it to find the third side.
Example: Consider a triangle with sides a = 7cm, b = 8cm, and c = 9cm. To find angle A, we use the Cosine Rule:
7² = 8² + 9² - 2 * 8 * 9 * cos A
cos A = (8² + 9² - 7²) / (2 * 8 * 9) ≈ 0.6597
A = arccos(0.6597) ≈ 48.6°
Why the Sine and Cosine Rules Work
The beauty of the Sine and Cosine Rules lies in their derivation, which subtly employs the principles behind SOHCAHTOA but in a more generalized way. They often involve constructing auxiliary lines within the triangle to create right-angled triangles, allowing the application of SOHCAHTOA to specific parts, then ultimately combining the results to yield the Sine and Cosine Rules. The process, while not directly employing SOHCAHTOA on the original non-right triangle, leverages its core principles in a sophisticated manner. This demonstrates the underlying unity within trigonometry, showing how even "advanced" rules build upon fundamental concepts.
Ambiguous Cases in Non-Right Triangles
The Sine Rule, when used with two sides and an angle opposite one of them (SSA), can lead to ambiguous cases. This means there might be two possible triangles that fulfill the given conditions. This ambiguity arises because the angle given might have two potential positions within the triangle, leading to different solutions for the remaining sides and angles. Careful analysis of the given information, possibly including considerations of side lengths relative to each other, is crucial to determine if a valid solution exists and if it's unique.
Practical Applications: When to Use Which Rule
The choice between the Sine Rule and the Cosine Rule depends entirely on the information provided:
-
Use the Sine Rule if you know:
- Two angles and one side (AAS or ASA)
- Two sides and an angle opposite one of them (SSA – be aware of ambiguity!)
-
Use the Cosine Rule if you know:
- Three sides (SSS)
- Two sides and the included angle (SAS)
Beyond SOHCAHTOA: Expanding Trigonometric Horizons
While SOHCAHTOA serves as a fantastic introduction to trigonometry and is invaluable for right-angled triangles, understanding and applying the Sine and Cosine Rules opens up a world of possibilities for solving problems involving any triangle. These more generalized rules form the foundation for many advanced trigonometric concepts and applications in various fields like surveying, navigation, physics, and engineering.
Area of a Triangle: Another Important Formula
It's worth mentioning another crucial formula for non-right triangles: the area formula. The area of any triangle can be calculated using:
Area = (1/2)ab sin C
(where a and b are two sides, and C is the angle between them). This formula elegantly combines concepts from SOHCAHTOA (the sine function) within a context applicable to all triangles.
Conclusion: SOHCAHTOA's Role in a Broader Context
SOHCAHTOA, while not directly applicable to non-right triangles, isn't rendered obsolete. Its underlying principles are fundamental and are implicitly used in the derivation of the Sine and Cosine Rules. Understanding these more general laws allows for the complete solution of any triangle problem, extending the reach and power of trigonometric concepts beyond the confines of right-angled triangles. Remember to choose the appropriate rule based on the given information, always being mindful of potential ambiguities when using the Sine Rule with SSA data. The journey from SOHCAHTOA to the Sine and Cosine Rules represents a natural progression in mastering trigonometric problem-solving. Mastering both is essential for a thorough understanding of trigonometry and its applications.
Latest Posts
Latest Posts
-
Prokaryotes That Obtain Their Energy From Chemical Compounds Are Called
Apr 04, 2025
-
What Does High Absorbance Mean In Spectrophotometry
Apr 04, 2025
-
Electric Field Due To A Disk Of Charge
Apr 04, 2025
-
Compare And Contrast Skeletal Smooth And Cardiac Muscle
Apr 04, 2025
-
The Integuments Of The Ovule Develop Into The
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Does Sohcahtoa Work On Non Right Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
