Each Orbital Can Hold How Many Electrons
Muz Play
Apr 03, 2025 · 5 min read
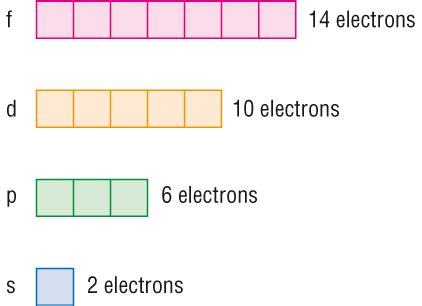
Table of Contents
Each Orbital Can Hold How Many Electrons? A Deep Dive into Atomic Structure
Understanding how many electrons each orbital can hold is fundamental to grasping the basics of chemistry and atomic structure. This seemingly simple question opens the door to a fascinating exploration of quantum mechanics and the behavior of matter at the subatomic level. Let's delve into the details, unraveling the mysteries behind electron configuration and the Pauli Exclusion Principle.
The Fundamentals: Orbitals and Quantum Numbers
Before we answer the central question, let's establish a firm foundation. Atoms are composed of a nucleus containing protons and neutrons, surrounded by a cloud of electrons. These electrons don't orbit the nucleus in neat, predictable paths like planets around a star. Instead, they exist in regions of space called orbitals.
These orbitals aren't simply random spaces; their shapes and energies are defined by a set of quantum numbers. These numbers provide a unique "address" for each electron within an atom. The four main quantum numbers are:
-
Principal Quantum Number (n): This number dictates the energy level of the electron and the size of the orbital. It's a positive integer (n = 1, 2, 3,...). Higher values of n represent higher energy levels and larger orbitals further from the nucleus.
-
Azimuthal Quantum Number (l): This describes the shape of the orbital and its angular momentum. It can take integer values from 0 to n - 1. l = 0 corresponds to an s orbital (spherical), l = 1 to a p orbital (dumbbell-shaped), l = 2 to a d orbital (more complex shapes), and l = 3 to an f orbital (even more complex shapes).
-
Magnetic Quantum Number (ml): This specifies the orientation of the orbital in space. It can take integer values from -l to +l, including 0. For example, a p orbital (l = 1) has three possible orientations (ml = -1, 0, +1), often designated as px, py, and pz.
-
Spin Quantum Number (ms): This describes the intrinsic angular momentum of the electron, often visualized as a spinning motion. It can only have two values: +1/2 (spin up, ↑) or -1/2 (spin down, ↓).
The Pauli Exclusion Principle: The Key to Orbital Occupancy
The crucial principle governing how many electrons can occupy an orbital is the Pauli Exclusion Principle. This principle states that no two electrons in an atom can have the same set of four quantum numbers. In simpler terms, each electron must have a unique "address" within the atom.
Since the first three quantum numbers (n, l, ml) define a specific orbital, the only remaining quantum number is the spin quantum number (ms). This means that each orbital can hold a maximum of two electrons, one with spin up (+1/2) and one with spin down (-1/2).
Orbital Occupancy and Electron Configuration
The Pauli Exclusion Principle directly dictates how electrons fill orbitals within an atom. This filling process follows a specific order, generally determined by increasing energy levels. This order is often represented by the Aufbau principle (although exceptions exist for heavier elements). Let's consider some examples:
-
Hydrogen (H): Hydrogen has one electron, which occupies the lowest energy level orbital, the 1s orbital.
-
Helium (He): Helium has two electrons, both occupying the 1s orbital, one with spin up and one with spin down. The 1s orbital is now filled.
-
Lithium (Li): Lithium has three electrons. Two fill the 1s orbital, and the third electron occupies the next lowest energy level orbital, the 2s orbital.
-
Carbon (C): Carbon has six electrons. Two fill the 1s orbital, two fill the 2s orbital, and the remaining two electrons occupy two of the three 2p orbitals, each with a single electron to minimize electron-electron repulsion (Hund's rule).
This filling pattern continues for all elements, with electrons filling orbitals according to their energy levels and the Pauli Exclusion Principle. The order of filling is often depicted using a diagram called an electron configuration diagram, utilizing subshells (s, p, d, f).
Beyond the Basics: Degeneracy and Electron-Electron Interactions
The simple picture of orbital filling presented above is an idealization. In reality, electron-electron interactions and other factors can influence the energy levels of orbitals, leading to some complexities.
Degeneracy: Orbitals with the same principal quantum number (n) and azimuthal quantum number (l) are said to be degenerate. This means they have the same energy level. For example, the three 2p orbitals (px, py, pz) are degenerate. However, this degeneracy can be broken by factors like the presence of other electrons or external magnetic fields.
Electron-Electron Repulsion: Electrons repel each other due to their negative charge. This repulsion affects the energy levels and the spatial distribution of electrons within the atom. Hund's rule, mentioned earlier, reflects this effect. Electrons will tend to occupy different orbitals within a subshell before pairing up in the same orbital to minimize repulsion.
Applications and Significance
Understanding the maximum occupancy of orbitals is crucial in various fields:
-
Chemistry: It's fundamental to predicting chemical bonding, reactivity, and the properties of molecules. The electron configuration of an atom dictates how it will interact with other atoms.
-
Materials Science: The electronic structure of materials, determined by orbital occupancy, is directly related to their electrical, magnetic, and optical properties. This knowledge is essential for designing new materials with specific functionalities.
-
Spectroscopy: The interaction of light with atoms and molecules is governed by electron transitions between different energy levels and orbitals. Spectroscopic techniques utilize this principle to analyze the composition and structure of matter.
-
Nuclear Physics: Understanding electron configurations is vital in studying nuclear reactions and the behavior of radioactive isotopes.
Conclusion: A Simple Principle with Profound Implications
The simple answer to the question "Each orbital can hold how many electrons?" is two. However, the underlying principles and implications are far-reaching. The Pauli Exclusion Principle, coupled with the concepts of quantum numbers and electron-electron interactions, provides a framework for understanding the complex world of atomic structure and its influence on the macroscopic properties of matter. This knowledge is fundamental to many scientific disciplines and continues to drive advancements in technology and our understanding of the universe. The seemingly simple capacity of an orbital to hold two electrons forms the bedrock of modern chemistry and physics, reminding us that even the smallest details can have the most significant consequences.
Latest Posts
Latest Posts
-
Dna Biology And Technology Dna And Rna Structure
Apr 04, 2025
-
Narcotics Act On The Central Nervous System By Producing A
Apr 04, 2025
-
Two Plants Heteroygous For Pod Color Are Crossed Refer To
Apr 04, 2025
-
What Two Main Products Result From Photosynthesis
Apr 04, 2025
-
Identify What A Coffee Cup Calorimeter Measures
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Each Orbital Can Hold How Many Electrons . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
