Electric Field Due To Disk Of Charge
Muz Play
Apr 02, 2025 · 6 min read
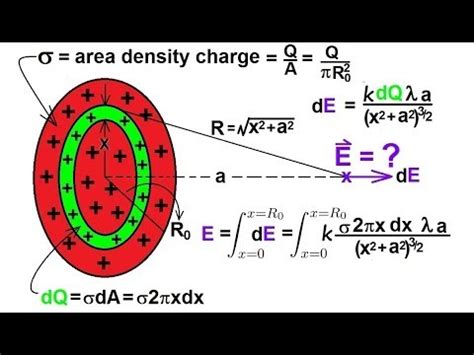
Table of Contents
Electric Field Due to a Disk of Charge: A Comprehensive Guide
Calculating the electric field due to a continuous charge distribution, like a disk, requires a slightly different approach than calculating the field due to a point charge. Instead of a simple Coulomb's Law application, we need to employ integration techniques. This article will provide a comprehensive guide to understanding and calculating the electric field produced by a uniformly charged disk, covering various aspects from the fundamental principles to advanced considerations.
Understanding the Problem: From Point Charges to Continuous Distributions
Before delving into the specifics of a charged disk, let's revisit the concept of the electric field due to a point charge. Coulomb's Law elegantly describes this:
E = kQ/r²
where:
- E represents the electric field strength.
- k is Coulomb's constant (approximately 8.98755 × 10⁹ N⋅m²/C²).
- Q is the magnitude of the point charge.
- r is the distance from the point charge to the point where the electric field is being measured.
However, a disk of charge isn't a point charge. It's a continuous distribution of charge spread across a two-dimensional surface. To handle this, we need to break the disk into infinitesimally small charge elements, treat each element as a point charge, and then integrate the contributions of all these elements to find the total electric field.
Setting up the Integration: Defining Variables and Charge Density
Consider a uniformly charged disk with radius R and total charge Q. The surface charge density (σ), which represents the charge per unit area, is constant across the disk and is given by:
σ = Q / (πR²)
Now, let's consider a small ring-shaped element within the disk, with radius r and width dr. The area of this ring is approximately 2πr dr. The charge (dQ) contained within this ring is:
dQ = σ(2πr dr)
This small charge element can be treated as a point charge for the purpose of calculating its contribution to the electric field at a point P located on the axis of the disk at a distance z from its center.
Calculating the Electric Field Component along the Axis
The electric field (dE) due to the small charge element dQ at point P has two components: one along the axis of the disk (dE<sub>z</sub>) and one perpendicular to the axis (dE<sub>⊥</sub>). Due to symmetry, the perpendicular components from all the ring elements cancel each other out. Therefore, we only need to consider the axial component:
dE<sub>z</sub> = (k dQ cosθ) / (r² + z²)
where θ is the angle between the line connecting the charge element to point P and the axis of the disk. Using trigonometry, we can express cosθ as:
cosθ = z / √(r² + z²)
Substituting the expressions for dQ and cosθ into the equation for dE<sub>z</sub>, we get:
dE<sub>z</sub> = (k σ z (2πr dr)) / ((r² + z²)^(3/2))
Performing the Integration: Finding the Total Electric Field
Now, we integrate dE<sub>z</sub> over the entire disk (from r = 0 to r = R) to find the total electric field along the z-axis at point P:
E<sub>z</sub> = ∫ dE<sub>z</sub> = ∫₀ᴿ (k σ z (2πr dr)) / ((r² + z²)^(3/2))
This integral can be solved using a substitution method (let u = r² + z²). After performing the integration, we obtain the final expression for the electric field along the axis of the uniformly charged disk:
E<sub>z</sub> = 2πkσ [1 - z / √(R² + z²)]
This equation shows that the electric field along the axis of a uniformly charged disk depends on the surface charge density (σ), the distance from the center of the disk (z), and the radius of the disk (R).
Analyzing the Results: Limiting Cases and Interpretations
Let's analyze some limiting cases to understand the behavior of the electric field:
-
z >> R (Far away from the disk): In this case, the term z/√(R² + z²) approaches 1, and the expression simplifies to:
E<sub>z</sub> ≈ 0
This makes intuitive sense; from a large distance, the disk appears as a point charge with zero net dipole moment, resulting in a negligible field.
-
z << R (Close to the disk): The term z/√(R² + z²) approaches 0, and the expression simplifies to:
E<sub>z</sub> ≈ 2πkσ = σ / (2ε₀)
This indicates that the electric field close to the disk becomes independent of the distance z and is directly proportional to the surface charge density. This resembles the electric field near an infinitely large charged plane.
-
R → ∞ (Infinitely large disk): As the radius of the disk approaches infinity, the term z/√(R² + z²) tends to zero, leading to:
E<sub>z</sub> ≈ 2πkσ = σ / (2ε₀)
This result confirms that the electric field near an infinitely large, uniformly charged plane is independent of the distance from the plane.
Beyond the Axis: Electric Field at Off-Axis Points
Calculating the electric field at points off the axis of the disk is significantly more complex. The symmetry that allowed us to ignore the perpendicular components no longer exists. The integration becomes a two-dimensional integral, involving both radial and angular coordinates. While solvable, this calculation often requires more advanced mathematical techniques and is beyond the scope of a basic introductory physics treatment.
Applications and Significance
The concept of the electric field due to a disk of charge has numerous applications in various fields, including:
-
Electrostatics: Understanding this concept is crucial for analyzing the behavior of capacitors, which often involve charged plates or disks.
-
Particle Physics: Charged particle beams often interact with detector elements that can be modeled as disks.
-
Plasma Physics: Charged particle distributions in plasmas can sometimes be approximated as disks for simplified calculations.
-
Astronomy and Astrophysics: Charged dust clouds or other celestial bodies can be approximated as disks for understanding their electromagnetic interactions.
Conclusion: A Powerful Tool for Understanding Electric Fields
Calculating the electric field due to a disk of charge is a fundamental problem in electrostatics that showcases the power and necessity of integration techniques in handling continuous charge distributions. While the axial calculation is relatively straightforward, understanding the limitations and exploring the more complex off-axis calculations demonstrates the depth and richness of this topic. Mastering this concept provides a solid foundation for further exploration of more sophisticated electromagnetic phenomena. The various limiting cases explored highlight the relationship between the electric field produced by a disk and those of simpler charge distributions, such as point charges and infinite planes. This understanding is crucial for tackling more complicated problems in electromagnetism and its numerous applications. The ability to visualize and manipulate the integral expressions allows for a deeper understanding of the physics involved. Beyond the calculations, understanding the implications and applications of this concept further strengthens one's grasp of electromagnetism and its importance in the real world.
Latest Posts
Latest Posts
-
Cis 1 3 Dimethylcyclohexane Chair Conformation
Apr 03, 2025
-
What Does The Bacterial Chromosome Do
Apr 03, 2025
-
What Is The Difference Between Dehydration And Hydrolysis
Apr 03, 2025
-
What Is The Most Complex Level Of Organization
Apr 03, 2025
-
What Determines The Volume Of Gas
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Due To Disk Of Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
