Electric Field Due To Ring Of Charge
Muz Play
Mar 31, 2025 · 5 min read
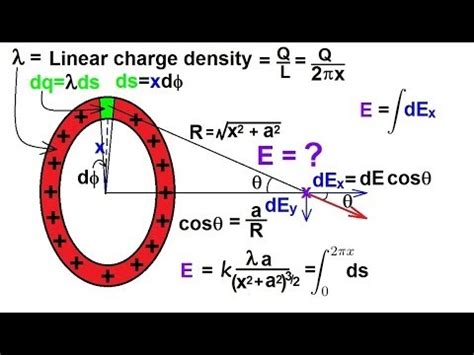
Table of Contents
Electric Field Due to a Ring of Charge: A Comprehensive Guide
The electric field, a fundamental concept in electromagnetism, describes the influence of a charged object on its surroundings. Understanding how to calculate the electric field generated by various charge distributions is crucial in physics and engineering. This article delves into the intricacies of calculating the electric field due to a ring of charge, a classic problem that elegantly demonstrates the application of Coulomb's law and vector calculus. We will explore the derivation, analyze special cases, and discuss the implications of this calculation.
Understanding the Problem: A Ring of Charge
Imagine a thin, uniformly charged ring of radius 'R' carrying a total charge 'Q'. Our goal is to determine the electric field at any point in space, particularly focusing on points along the axis of symmetry (the z-axis) and at arbitrary points in space.
Coulomb's Law: The Foundation
The cornerstone of our calculation is Coulomb's Law, which states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. Mathematically:
F = k * |q1 * q2| / r²
where:
- F is the force between the charges
- k is Coulomb's constant (approximately 8.98755 × 10⁹ N⋅m²/C²)
- q1 and q2 are the magnitudes of the charges
- r is the distance between the charges
This law forms the basis for understanding electric fields, which can be defined as the force per unit charge experienced by a test charge placed in the field.
Calculating the Electric Field Along the Axis of Symmetry (z-axis)
This is the most straightforward case. Let's consider a point P located at a distance 'z' along the axis of the ring from its center.
1. Symmetry and Simplification
Due to the symmetry of the ring, the components of the electric field perpendicular to the z-axis cancel each other out. This simplification drastically reduces the complexity of the calculation. We only need to consider the z-component of the electric field.
2. Consider a Small Charge Element
Let's divide the ring into infinitesimally small charge elements, dq. Each dq contributes a small electric field, dE, at point P.
3. Calculating the z-component of dE
The distance between dq and point P is given by:
r = √(R² + z²)
The z-component of dE is given by:
dEz = dE * cos(θ)
where θ is the angle between the line connecting dq and P and the z-axis. Using trigonometry, we have:
cos(θ) = z / √(R² + z²)
Therefore:
dEz = (k * dq / (R² + z²)) * (z / √(R² + z²)) = k * z * dq / (R² + z²)^(3/2)
4. Integration to Find the Total Electric Field
To find the total electric field Ez at point P, we integrate dEz over the entire ring:
Ez = ∫ dEz = ∫ (k * z * dq / (R² + z²)^(3/2))
Since k and z are constants, we can take them outside the integral:
Ez = (k * z / (R² + z²)^(3/2)) ∫ dq
The integral of dq over the entire ring is simply the total charge Q:
Ez = (k * Q * z) / (R² + z²)^(3/2)
This is the final expression for the electric field along the axis of symmetry of a charged ring.
Analyzing the Result: Special Cases and Implications
Let's examine some interesting scenarios:
1. At the Center of the Ring (z = 0)
When z = 0, the electric field along the z-axis is:
Ez = 0
This is intuitively expected due to the symmetry of the ring. The electric field contributions from opposite sides cancel each other out.
2. Far Away from the Ring (z >> R)
When z is much greater than R, the term R² in the denominator can be neglected:
Ez ≈ (k * Q * z) / z³ = k * Q / z²
This resembles the electric field of a point charge Q located at the origin. At large distances, the ring effectively behaves like a point charge.
3. Close to the Ring (z << R)
When z is much smaller than R, the expression becomes:
Ez ≈ (k * Q * z) / R³
The electric field is approximately proportional to z, indicating a linear relationship between the field and the distance from the center of the ring near the ring itself.
Calculating the Electric Field at an Arbitrary Point in Space
Calculating the electric field at an arbitrary point in space is considerably more complex. It involves resolving the electric field into its x, y, and z components and integrating over the entire ring. This typically involves using double integrals and cylindrical coordinates, resulting in a more intricate mathematical derivation. While the process is more involved, the fundamental principles remain the same: applying Coulomb's law to infinitesimal charge elements and integrating over the entire charge distribution. The solution often involves elliptic integrals, making it a more advanced mathematical problem.
Applications and Significance
The study of the electric field due to a ring of charge is not merely a theoretical exercise. It has numerous practical applications and helps build a foundational understanding for more complex scenarios:
- Antenna Design: Understanding the electric field distribution is crucial in the design of antennas and other electromagnetic devices.
- Particle Accelerators: The electric fields generated by various charge configurations are essential in designing particle accelerators.
- Electrostatic Lenses: Electrostatic lenses, used in electron microscopes and other instruments, rely on carefully controlled electric fields to focus beams of charged particles.
- Fundamental Physics: Understanding the electric field of simple charge distributions is a building block for tackling more complex problems in electromagnetism and related fields.
Conclusion: A Stepping Stone to Deeper Understanding
Calculating the electric field due to a ring of charge, particularly along its axis of symmetry, provides a valuable illustration of the application of Coulomb's law and integration techniques. This problem showcases the power of symmetry arguments in simplifying complex calculations and allows for a deeper understanding of electric field behavior. While the arbitrary point calculation presents a greater mathematical challenge, it reinforces the fundamental principles and highlights the richness and complexity of electromagnetism. Mastering this concept serves as a strong foundation for tackling more advanced problems in electrostatics and electrodynamics. Further exploration might involve studying the electric potential due to a ring of charge, which provides an alternative approach to calculating the electric field using the relationship between electric field and potential.
Latest Posts
Latest Posts
-
Who Is Credited With Discovering Cells
Apr 02, 2025
-
Calculate The Ph At The Equivalence Point For The Titration
Apr 02, 2025
-
Gramatica A The Verb Tener Answers
Apr 02, 2025
-
Are There Lysosomes In A Plant Cell
Apr 02, 2025
-
Root System And Shoot System Of Plants
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Due To Ring Of Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
