Electric Field Of A Charged Disk
Muz Play
Mar 31, 2025 · 6 min read
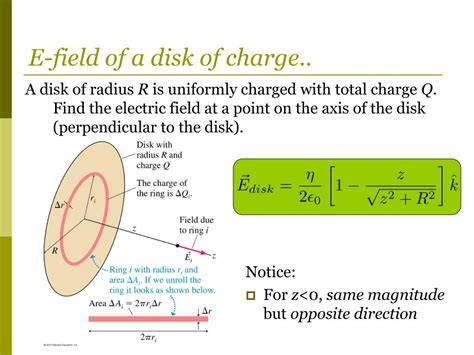
Table of Contents
Electric Field of a Charged Disk: A Comprehensive Guide
The electric field, a fundamental concept in electromagnetism, describes the force exerted on a charged particle. Calculating the electric field for various charge distributions is crucial in understanding many physical phenomena. This article delves into the intricacies of calculating the electric field produced by a uniformly charged disk, exploring different approaches and offering a comprehensive understanding of the underlying principles. We'll examine both the on-axis and off-axis fields, highlighting the mathematical techniques involved and their practical implications.
Understanding the Basics: Electric Field and Charge Distribution
Before embarking on the calculation for a charged disk, let's briefly review some fundamental concepts.
Electric Field: A Force Field
The electric field (E) at a point in space is defined as the force per unit charge experienced by a small positive test charge placed at that point. It's a vector quantity, meaning it has both magnitude and direction. The direction of the electric field points in the direction of the force that would be exerted on a positive test charge. Mathematically, it's represented as:
E = F/q
where:
- E is the electric field
- F is the force on the test charge
- q is the magnitude of the test charge
Coulomb's Law: The Foundation of Electrostatics
Coulomb's Law is the cornerstone of electrostatics, describing the force between two point charges. The force is directly proportional to the product of the charges and inversely proportional to the square of the distance separating them:
F = k * |q1 * q2| / r²
where:
- F is the force between the two charges
- k is Coulomb's constant (approximately 8.98755 × 10⁹ N⋅m²/C²)
- q1 and q2 are the magnitudes of the two charges
- r is the distance between the two charges
Charge Density: Describing Charge Distribution
For continuous charge distributions, such as a charged disk, it's more convenient to work with charge density. This quantifies how much charge is packed into a given volume (volume charge density, ρ), area (surface charge density, σ), or length (linear charge density, λ). For a uniformly charged disk, we'll primarily use surface charge density, σ, which is defined as:
σ = Q/A
where:
- σ is the surface charge density
- Q is the total charge on the disk
- A is the area of the disk
Calculating the Electric Field of a Charged Disk: On-Axis Case
Let's begin by considering the simplest scenario: calculating the electric field along the axis of symmetry of a uniformly charged disk. This involves integrating the contributions from infinitesimal charge elements across the disk's surface.
Setting up the Integration
Consider a thin ring of radius r and infinitesimal width dr on the disk. The area of this ring is 2πr dr. The charge dq on this ring is given by:
dq = σ * 2πr dr
The electric field dE due to this infinitesimal ring at a point z along the axis of the disk can be calculated using Coulomb's Law and symmetry considerations. The components of dE perpendicular to the axis cancel out, leaving only the z-component:
dE<sub>z</sub> = (k * dq * z) / (z² + r²)<sup>3/2</sup>
Substituting the expression for dq, we get:
dE<sub>z</sub> = (k * σ * 2πr * z * dr) / (z² + r²)<sup>3/2</sup>
Performing the Integration
To find the total electric field E<sub>z</sub> along the axis, we integrate dE<sub>z</sub> over the entire disk (from r = 0 to r = R, where R is the radius of the disk):
E<sub>z</sub> = ∫ dE<sub>z</sub> = ∫<sub>0</sub><sup>R</sup> (k * σ * 2πr * z * dr) / (z² + r²)<sup>3/2</sup>
This integral can be solved using a simple substitution (u = z² + r², du = 2r dr), yielding:
E<sub>z</sub> = 2πkσ [1 - z / √(z² + R²)]
This equation gives the electric field along the axis of a uniformly charged disk. Notice that as z becomes much larger than R (far away from the disk), the electric field approaches that of a point charge with a magnitude equal to the total charge on the disk.
Calculating the Electric Field of a Charged Disk: Off-Axis Case
Calculating the electric field at points off the axis of symmetry is significantly more challenging. It requires a more complex integration process, often involving elliptical integrals.
The Complexity of Off-Axis Calculation
The symmetry that simplifies the on-axis calculation is lost when considering off-axis points. Each infinitesimal charge element on the disk contributes a vector electric field, and the integration must account for both the magnitude and direction of each contribution. This results in a vector integral that is considerably more difficult to solve analytically.
Approximations and Numerical Methods
For off-axis points, numerical methods or approximations are often necessary. Numerical techniques, such as Monte Carlo integration or finite element analysis, provide accurate solutions but require computational power. Approximations might involve considering the disk as a collection of discrete point charges or using series expansions, but accuracy depends on the proximity of the point to the disk.
Applications and Significance
The electric field of a charged disk has several practical applications and theoretical significances:
- Modeling Capacitors: Parallel plate capacitors, a fundamental component in electronics, can be approximated as two charged disks facing each other. The electric field calculation helps determine the capacitance and potential difference.
- Understanding Charged Particle Beams: Understanding the electric field of a charged disk is vital in designing and analyzing charged particle accelerators and other devices that manipulate charged particle beams.
- Electrostatic Lenses: In electron microscopy and other applications, electrostatic lenses use shaped electrodes to focus electron beams. The electric field generated by these electrodes, often resembling a charged disk, plays a crucial role in focusing the beams.
- Theoretical Physics: The charged disk problem serves as a valuable example in electromagnetism, illustrating the application of integration techniques and the complexities of dealing with continuous charge distributions.
Further Exploration and Advanced Topics
The analysis presented here focuses on a uniformly charged disk. The calculations become considerably more complex for non-uniform charge distributions. Exploring these advanced topics requires a strong foundation in vector calculus and integral techniques.
Conclusion
Calculating the electric field of a charged disk, particularly the off-axis case, presents a significant mathematical challenge. However, understanding the fundamental principles and the different approaches for solving the on-axis case provides a solid foundation for tackling more complex scenarios and appreciating the practical applications of this problem in various fields of physics and engineering. The simplicity of the on-axis calculation and the inherent complexity of the off-axis calculation showcase the subtle yet powerful interplay between geometry and the electric field. Through a deeper understanding of these concepts, one can appreciate the intricate nature of electromagnetism and its profound impact on our understanding of the physical world. The ability to calculate and visualize electric fields is essential for the design and analysis of a vast array of electronic devices and physical systems. This understanding is crucial for advancing technological capabilities and expanding the boundaries of scientific knowledge.
Latest Posts
Latest Posts
-
How Does The Nucleus And Ribosomes Work Together
Apr 01, 2025
-
Having A Single Set Of Unpaired Chromosomes
Apr 01, 2025
-
How To Calculate Current In A Series Circuit
Apr 01, 2025
-
Unity Of Life And Diversity Of Life
Apr 01, 2025
-
Choose The Most Likely Correlation Value For This Scatterplot
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of A Charged Disk . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
