Evaluate The Integral By Changing To Spherical Coordinates
Muz Play
Mar 27, 2025 · 5 min read
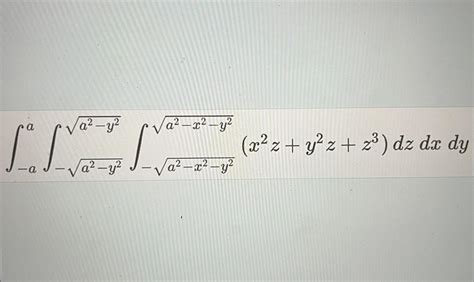
Table of Contents
Evaluating Integrals by Changing to Spherical Coordinates: A Comprehensive Guide
Changing to spherical coordinates is a powerful technique for evaluating triple integrals, particularly those involving regions that possess spherical symmetry. This method significantly simplifies the integration process by transforming a complex Cartesian integral into a more manageable spherical integral. This comprehensive guide will delve into the intricacies of spherical coordinate transformations, providing a step-by-step approach with practical examples.
Understanding Spherical Coordinates
Before diving into the integration process, let's establish a solid understanding of spherical coordinates. While Cartesian coordinates use x, y, and z to locate a point in three-dimensional space, spherical coordinates utilize three parameters:
- ρ (rho): The radial distance from the origin to the point. This is always a non-negative value (ρ ≥ 0).
- φ (phi): The polar angle, measured from the positive z-axis down to the projection of the point onto the xy-plane. This angle typically ranges from 0 to π (0 ≤ φ ≤ π).
- θ (theta): The azimuthal angle, measured from the positive x-axis in the xy-plane to the projection of the point onto the xy-plane. This angle usually ranges from 0 to 2π (0 ≤ θ ≤ 2π).
The conversion between Cartesian and spherical coordinates is defined by the following equations:
- x = ρsinφcosθ
- y = ρsinφsinθ
- z = ρcosφ
Conversely, to find spherical coordinates from Cartesian coordinates:
- ρ = √(x² + y² + z²)
- φ = arccos(z/ρ)
- θ = arctan(y/x) (Note: Careful consideration is needed for the quadrants of x and y to determine the correct value of θ)
The Jacobian determinant, essential for changing variables in multiple integrals, for the transformation from Cartesian to spherical coordinates is ρ²sinφ. This factor accounts for the scaling of the infinitesimal volume element. Therefore, the volume element dV in spherical coordinates becomes:
dV = ρ²sinφ dρ dφ dθ
The Process of Converting and Evaluating Triple Integrals
The process of evaluating a triple integral by changing to spherical coordinates involves several key steps:
-
Identify the Region of Integration: Carefully examine the region of integration defined by the limits of the Cartesian integral. Sketching the region can be immensely helpful. Look for spherical symmetry—regions defined by spheres, cones, or portions thereof are prime candidates for this transformation.
-
Convert the Limits of Integration: Express the limits of integration in terms of ρ, φ, and θ. This step requires a careful analysis of the region's boundaries. Often, it's easier to determine the limits for ρ first, followed by φ, and then θ.
-
Transform the Integrand: Substitute the expressions for x, y, and z in terms of ρ, φ, and θ into the integrand. Remember to also incorporate the Jacobian determinant (ρ²sinφ).
-
Evaluate the Iterated Integral: Evaluate the resulting iterated integral with respect to ρ, φ, and θ, in that order (or any order that simplifies the calculation).
Example Problems: A Step-by-Step Guide
Let's illustrate the process with a few examples of increasing complexity:
Example 1: Simple Sphere
Evaluate the triple integral ∫∫∫<sub>E</sub> (x² + y² + z²) dV, where E is the unit ball x² + y² + z² ≤ 1.
-
Region: The region E is a sphere with radius 1 centered at the origin.
-
Limits: 0 ≤ ρ ≤ 1, 0 ≤ φ ≤ π, 0 ≤ θ ≤ 2π
-
Integrand: x² + y² + z² = ρ². The integral becomes ∫∫∫ ρ² (ρ²sinφ dρ dφ dθ)
-
Evaluation:
∫<sub>0</sub><sup>2π</sup> ∫<sub>0</sub><sup>π</sup> ∫<sub>0</sub><sup>1</sup> ρ⁴sinφ dρ dφ dθ = ∫<sub>0</sub><sup>2π</sup> dθ ∫<sub>0</sub><sup>π</sup> sinφ dφ ∫<sub>0</sub><sup>1</sup> ρ⁴ dρ = (2π)(-cosφ)|<sub>0</sub><sup>π</sup> (ρ⁵/5)|<sub>0</sub><sup>1</sup> = (2π)(2)(1/5) = 4π/5
Example 2: Cone and Sphere
Evaluate ∫∫∫<sub>E</sub> z dV, where E is the region bounded by the sphere x² + y² + z² = 1 and the cone z = √(x² + y²).
-
Region: This region lies within the unit sphere and above the cone.
-
Limits: The cone z = √(x² + y²) corresponds to φ = π/4 in spherical coordinates. Thus, the limits are 0 ≤ ρ ≤ 1, 0 ≤ φ ≤ π/4, 0 ≤ θ ≤ 2π.
-
Integrand: The integrand z becomes ρcosφ. The integral becomes ∫∫∫ ρcosφ (ρ²sinφ dρ dφ dθ).
-
Evaluation:
∫<sub>0</sub><sup>2π</sup> ∫<sub>0</sub><sup>π/4</sup> ∫<sub>0</sub><sup>1</sup> ρ³cosφsinφ dρ dφ dθ = ∫<sub>0</sub><sup>2π</sup> dθ ∫<sub>0</sub><sup>π/4</sup> cosφsinφ dφ ∫<sub>0</sub><sup>1</sup> ρ³ dρ = (2π)(1/2 sin²φ)|<sub>0</sub><sup>π/4</sup> (ρ⁴/4)|<sub>0</sub><sup>1</sup> = (2π)(1/4)(1/4) = π/8
Example 3: More Complex Region
Let's consider a region defined by 1 ≤ x² + y² + z² ≤ 4 and z ≥ √(x² + y²). This region lies between two spheres (radius 1 and 2) and above the cone.
-
Region: This region is the volume between two spheres and above a cone.
-
Limits: 1 ≤ ρ ≤ 2, 0 ≤ φ ≤ π/4, 0 ≤ θ ≤ 2π
-
Integrand: Suppose the integrand is simply 1 (finding the volume). The integral would be ∫∫∫ ρ²sinφ dρ dφ dθ
-
Evaluation: The evaluation would follow the same procedure as above, involving evaluating the iterated integral with the specified limits. The details are left as an exercise for the reader, but the key is setting up the correct limits based on the description of the region.
Advanced Considerations and Applications
The applications of spherical coordinates extend far beyond simple geometric shapes. They are crucial in various fields:
- Physics: Calculating gravitational or electrostatic potentials, analyzing electromagnetic fields, and solving problems in fluid dynamics.
- Engineering: Designing antennas, analyzing stress distributions in spherical structures, and modeling heat transfer.
- Computer Graphics: Rendering 3D scenes, creating realistic lighting effects, and simulating physical phenomena.
Dealing with Irregular Regions: For regions that are not perfectly symmetrical, careful consideration of the limits of integration is crucial. You may need to break the region into smaller, more manageable subregions.
Numerical Methods: If the resulting integral proves too complex to evaluate analytically, numerical integration techniques (like Simpson's rule or Gaussian quadrature) can be employed.
This detailed guide provides a solid foundation for understanding and applying spherical coordinates in evaluating triple integrals. By mastering these techniques, you unlock a powerful tool for solving a wide range of complex mathematical and physical problems. Remember the key steps: careful region analysis, correct limit determination, proper integrand transformation using the Jacobian, and methodical iterative integration. Practice is key to becoming proficient in this valuable calculus skill.
Latest Posts
Latest Posts
-
Work Done By A Varying Force
Mar 31, 2025
-
The Rna Components Of Ribosomes Are Synthesized In The
Mar 31, 2025
-
What Are The 2 Main Sources Of Genetic Variation
Mar 31, 2025
-
What Is A Reference Group In Sociology
Mar 31, 2025
-
Dividing Polynomials Math Lib Answer Key
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Integral By Changing To Spherical Coordinates . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
