Work Done By A Varying Force
Muz Play
Mar 31, 2025 · 5 min read
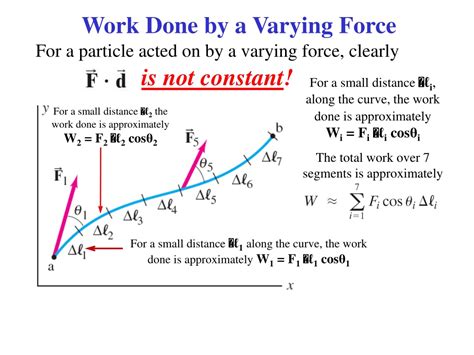
Table of Contents
- Work Done By A Varying Force
- Table of Contents
- Work Done by a Varying Force: A Comprehensive Guide
- Understanding Work and Energy
- Key Concepts:
- Calculating Work Done by a Varying Force
- 1. Graphical Method: Area Under the Curve
- 2. Calculus Method: Integration
- Examples of Varying Forces:
- Work Done by a Force at an Angle
- Applications of Work Done by Varying Forces
- 1. Engineering:
- 2. Physics:
- 3. Other Fields:
- Advanced Topics:
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Work Done by a Varying Force: A Comprehensive Guide
Understanding work done by a constant force is relatively straightforward: it's simply the force multiplied by the distance moved in the direction of the force (W = Fd). However, many real-world scenarios involve forces that change in magnitude or direction, making the calculation significantly more complex. This article provides a comprehensive exploration of work done by a varying force, covering both theoretical concepts and practical applications.
Understanding Work and Energy
Before delving into varying forces, let's solidify our understanding of the fundamental principles of work and energy. Work, in physics, is a measure of energy transfer that occurs when an object is moved over a distance by an external force. The energy of a system represents its capacity to do work. The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy.
Key Concepts:
- Scalar Quantity: Work is a scalar quantity, meaning it has magnitude but no direction. It's measured in Joules (J).
- Force and Displacement: Work depends on both the force applied and the displacement of the object. Only the component of the force parallel to the displacement contributes to the work done.
- Conservative and Non-conservative Forces: Conservative forces, like gravity, have the property that the work done is independent of the path taken. Non-conservative forces, like friction, depend on the path.
Calculating Work Done by a Varying Force
When dealing with a varying force, the simple formula W = Fd is insufficient. Instead, we must employ calculus to account for the continuous change in force.
1. Graphical Method: Area Under the Curve
A powerful way to visualize and calculate the work done by a varying force is to use a force-displacement graph. The work done is represented by the area under the force-displacement curve.
How it works:
- Plot the force (F) against displacement (x). The graph will show how the force varies as the object moves.
- Calculate the area. If the area is composed of regular shapes (like rectangles or triangles), calculating the area is straightforward. For irregular shapes, numerical integration methods (like the trapezoidal rule or Simpson's rule) or calculus are required.
Example: Imagine a spring. The force exerted by a spring is proportional to its extension (Hooke's Law: F = kx). The force-displacement graph would be a straight line. The area under the line (a triangle) represents the work done in stretching or compressing the spring.
2. Calculus Method: Integration
For more complex scenarios, calculus provides a precise method to determine the work done by a varying force. The work done is calculated using the following integral:
W = ∫ F(x) dx
Where:
- W is the work done
- F(x) is the force as a function of displacement (x)
- dx represents an infinitesimal displacement
This integral sums up the contributions of infinitesimally small amounts of work done over the entire displacement. Solving this integral requires knowledge of the specific function F(x) describing the varying force.
Examples of Varying Forces:
- Spring Force: As mentioned earlier, the force exerted by a spring varies linearly with its displacement. The integral for calculating work done in stretching or compressing a spring to a distance x is: W = (1/2)kx².
- Gravitational Force: The gravitational force varies inversely with the square of the distance from the center of the Earth (Newton's Law of Universal Gravitation). Calculating the work done in moving an object against gravity requires a more complex integral.
- Friction: While often modeled as a constant force, friction can actually vary depending on factors such as surface conditions and speed. Calculating work done against friction might involve a more sophisticated model that accounts for these variations.
- Electromagnetic Forces: Electric and magnetic forces can also vary with distance and other factors, requiring calculus for accurate work calculations.
Work Done by a Force at an Angle
In many real-world scenarios, the force isn't acting directly in the direction of motion. In such cases, only the component of the force parallel to the displacement contributes to the work done.
The formula for work done when the force is at an angle θ to the displacement is:
W = ∫ F(x)cos(θ) dx
Here, cos(θ) represents the component of the force that is parallel to the displacement. If the force and displacement are perpendicular (θ = 90°), then cos(θ) = 0, and no work is done.
Applications of Work Done by Varying Forces
Understanding work done by varying forces is crucial in many fields, including:
1. Engineering:
- Structural Analysis: Engineers use these principles to analyze the stresses and strains on structures subjected to varying loads.
- Machine Design: Designing efficient machines requires understanding the work done by varying forces in different components.
- Robotics: Planning robot movements necessitates accurate calculations of work done by actuators and other mechanisms.
2. Physics:
- Particle Physics: Understanding work done by varying electromagnetic fields is essential for studying particle interactions.
- Astrophysics: Calculating work done by gravitational forces is crucial for studying planetary orbits and stellar evolution.
3. Other Fields:
- Biomechanics: Analyzing human or animal movement often involves determining the work done by muscles and other biological structures.
- Meteorology: Understanding the work done by atmospheric pressure variations is important for modeling weather patterns.
Advanced Topics:
- Line Integrals: For forces that vary in both magnitude and direction along a curved path, line integrals are used to calculate the work done.
- Potential Energy: For conservative forces, the work done can be expressed in terms of potential energy, simplifying calculations significantly.
- Numerical Methods: When analytical solutions are difficult to obtain, numerical methods, such as finite element analysis, are employed to approximate the work done.
Conclusion
Calculating the work done by a varying force requires a deeper understanding of calculus and its applications. While the basic concept of work remains consistent – the transfer of energy during displacement – the mathematical tools needed become more sophisticated when the force is not constant. The methods described in this article provide a framework for addressing diverse problems, from simple spring systems to complex astrophysical phenomena. Mastering these concepts is fundamental to success in many scientific and engineering disciplines. Further exploration of the related fields mentioned will enhance the understanding of practical applications and deeper implications of this important principle.
Latest Posts
Latest Posts
-
Amino Acids Can Be Distinguished From One Another By
Apr 03, 2025
-
Balancing Equations Practice Worksheet With Answers
Apr 03, 2025
-
How Does The Predator Prey Relationship Affect A Population
Apr 03, 2025
-
The Axons Of Parasympathetic Postganglionic Neurons Are
Apr 03, 2025
-
Is Hydrogen A Metal Nonmetal Or Metalloid
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Work Done By A Varying Force . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
