Formula For Kinetic Energy Of A Spring
Muz Play
Apr 06, 2025 · 5 min read
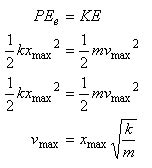
Table of Contents
The Formula for Kinetic Energy of a Spring: A Deep Dive
Understanding the kinetic energy of a spring system is crucial in various fields, from physics and engineering to robotics and material science. While the concept seems straightforward at first glance, a complete understanding requires delving into the nuances of spring mechanics, oscillatory motion, and energy conservation. This article will provide a comprehensive exploration of the kinetic energy formula for a spring, explaining its derivation, applications, and limitations.
Understanding Spring Potential Energy
Before we dive into the kinetic energy, it's crucial to grasp the concept of potential energy stored within a spring. A spring, when compressed or stretched from its equilibrium position, stores energy as potential energy. This potential energy is directly proportional to the square of the displacement from the equilibrium position. This relationship is described by the following formula:
PE = (1/2)kx²
Where:
- PE represents the potential energy stored in the spring (in Joules).
- k represents the spring constant (in Newtons per meter), a measure of the spring's stiffness. A higher spring constant indicates a stiffer spring.
- x represents the displacement from the equilibrium position (in meters).
This formula is fundamental to understanding the energy transformations within a spring-mass system.
The Interplay Between Potential and Kinetic Energy
When a spring is released from its compressed or stretched state, the stored potential energy begins to convert into kinetic energy. Kinetic energy is the energy of motion. As the spring oscillates, there's a continuous exchange between potential and kinetic energy. At the point of maximum displacement (maximum compression or extension), the kinetic energy is zero, and the potential energy is at its maximum. Conversely, at the equilibrium position (where x=0), the potential energy is zero, and the kinetic energy is at its maximum.
This continuous energy exchange is a key characteristic of simple harmonic motion (SHM), the type of oscillatory motion exhibited by a mass attached to an ideal spring.
Deriving the Kinetic Energy Formula
The kinetic energy of a mass attached to a spring can be derived using the principle of conservation of energy. The total mechanical energy (E) of the system remains constant, assuming no energy losses due to friction or other dissipative forces:
E = PE + KE
Where:
- E is the total mechanical energy.
- PE is the potential energy.
- KE is the kinetic energy.
Since the total energy is conserved, at any point in the oscillation, the sum of potential and kinetic energy remains constant. Therefore, we can express the kinetic energy as:
KE = E - PE
Substituting the formula for potential energy, we get:
KE = E - (1/2)kx²
To find the maximum kinetic energy, we consider the point where the potential energy is zero (at the equilibrium position, x=0). At this point, all the stored potential energy has been converted into kinetic energy. Therefore, the maximum kinetic energy is equal to the total mechanical energy:
KE_max = E
This means the maximum kinetic energy is equal to the initial potential energy stored in the spring when it was fully compressed or stretched:
KE_max = (1/2)kA²
where A is the amplitude (maximum displacement) of the oscillation.
Factors Affecting Kinetic Energy
Several factors influence the kinetic energy of a spring-mass system:
-
Spring Constant (k): A stiffer spring (higher k) will store more potential energy for the same displacement, resulting in a higher maximum kinetic energy.
-
Amplitude (A): A larger amplitude (greater displacement) implies more stored potential energy, leading to greater maximum kinetic energy.
-
Mass (m): While not directly present in the KE_max formula derived above, the mass of the object attached to the spring influences the oscillation frequency and velocity. A heavier mass will have a lower maximum velocity for the same amplitude, resulting in a lower maximum kinetic energy. The relationship is apparent through the equation for the angular frequency (ω) of the simple harmonic motion: ω = √(k/m).
-
Damping: In real-world scenarios, friction and other dissipative forces (damping) cause a gradual decrease in the amplitude and consequently reduce the kinetic energy over time.
Applications of the Kinetic Energy Formula
The formula for kinetic energy of a spring has wide-ranging applications:
-
Mechanical Engineering: Designing springs for various applications, such as suspension systems in vehicles or clock mechanisms, requires accurate calculations of energy storage and release.
-
Robotics: Understanding the kinetic energy of robotic arms and other moving components is critical for efficient movement control and energy management.
-
Material Science: Studying the mechanical properties of materials often involves analyzing the energy stored and released during deformation, relying heavily on spring-like models.
-
Physics Simulations: Accurate simulations of physical systems often require detailed modelling of energy transformations in spring-like elements.
Limitations of the Formula
It's important to acknowledge the limitations of the simple kinetic energy formula:
-
Ideal Spring Assumption: The formula assumes an ideal spring that obeys Hooke's Law perfectly. Real-world springs exhibit deviations from Hooke's Law at large displacements.
-
Neglect of Damping: The formula ignores energy losses due to friction and other dissipative forces, which are always present in real systems.
-
Neglect of other energy forms: The formula only considers potential and kinetic energy and neglects other forms of energy that may be involved, such as thermal energy generated due to friction.
Beyond the Basic Formula: More Complex Scenarios
In more complex scenarios, the simple formula may not suffice. For example:
-
Non-linear Springs: For springs that do not obey Hooke's Law, the potential energy function is no longer a simple quadratic, requiring more complex mathematical treatment.
-
Damped Oscillations: Incorporating damping effects necessitates the use of differential equations to model the system's behaviour.
-
Coupled Oscillators: Systems with multiple interacting springs and masses require advanced mathematical techniques to analyze the energy transfer and motion.
Conclusion: A Powerful Tool for Understanding Energy
The formula for the kinetic energy of a spring provides a fundamental understanding of energy transformations in oscillatory systems. While its application is often simplified by assumptions about ideal springs and negligible damping, it serves as a crucial building block for more sophisticated analyses of real-world spring systems. Understanding this fundamental concept is crucial for anyone working in fields involving mechanical systems, oscillations, and energy transfer. By recognizing both its power and its limitations, one can effectively utilize this formula to analyze and design a wide range of physical systems. The continued study and application of this fundamental formula contribute greatly to the advancement in diverse fields.
Latest Posts
Latest Posts
-
Instrument Used To Measure Length In Science
Apr 07, 2025
-
What Is A Compound Statement In Math
Apr 07, 2025
-
Lattice Energy Is An Estimate Of The Bond
Apr 07, 2025
-
What Are The Similarities Between Animal Cells And Plant Cells
Apr 07, 2025
-
Naming Compounds Practice Problems With Answers
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Formula For Kinetic Energy Of A Spring . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
