How Is Probability Used In Genetics
Muz Play
Apr 03, 2025 · 6 min read
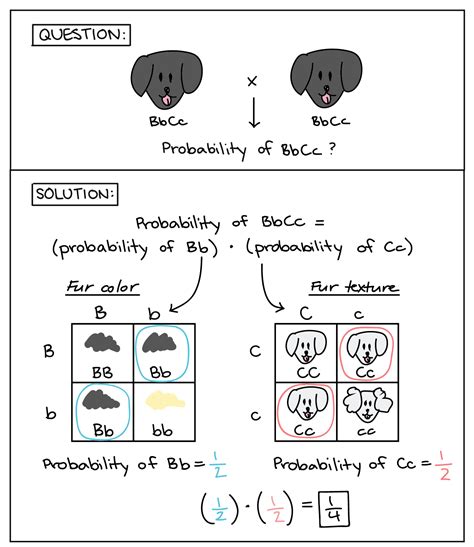
Table of Contents
How is Probability Used in Genetics?
Probability, the mathematical study of likelihood and chance, forms the bedrock of many genetic concepts. From predicting the inheritance patterns of traits in offspring to understanding the frequency of genetic disorders within populations, probability is an indispensable tool in the field of genetics. This article will delve into the various ways probability is utilized in genetics, exploring its applications in Mendelian inheritance, population genetics, and genetic counseling.
Mendelian Inheritance and Probability
Gregor Mendel's groundbreaking experiments with pea plants established the fundamental principles of inheritance. He observed that certain traits, like flower color or seed shape, were passed down from parents to offspring in predictable patterns. These patterns could be explained using the principles of probability.
Punnett Squares: A Visual Representation of Probability
One of the most widely used tools to visualize the probabilistic nature of inheritance is the Punnett Square. This simple diagram allows us to predict the genotypes and phenotypes of offspring based on the genotypes of the parents. For example, consider a monohybrid cross involving a homozygous dominant parent (AA) and a homozygous recessive parent (aa) for a particular trait.
- Parental Genotypes: AA x aa
- Possible Gametes: A and a
- Punnett Square:
| A | A | |
|---|---|---|
| a | Aa | Aa |
| a | Aa | Aa |
In this scenario, all offspring (100%) will have the heterozygous genotype (Aa) and will express the dominant phenotype. The Punnett Square illustrates the probabilistic certainty of this outcome.
Dihybrid and More Complex Crosses
The principles extend to dihybrid crosses (considering two traits simultaneously) and even more complex scenarios involving multiple genes. While the Punnett Squares become larger and more complex with increasing numbers of genes, the underlying principle of probability remains the same. We calculate the probability of each genotype and phenotype combination by multiplying the probabilities of individual gene pairings. For instance, in a dihybrid cross involving two heterozygous parents (AaBb x AaBb), we can determine the probability of offspring inheriting a specific genotype (e.g., AABB) by considering the independent assortment of alleles.
Beyond Simple Mendelian Inheritance: Considering Modifying Factors
While Mendelian inheritance provides a solid foundation, it's crucial to acknowledge that real-world inheritance patterns are often more intricate. Factors like incomplete dominance, codominance, pleiotropy (one gene influencing multiple traits), epistasis (interaction between multiple genes), and environmental influences can complicate the simple probabilistic predictions made using Punnett squares. However, even in these complex cases, probability remains a vital tool for understanding and quantifying the likelihood of different outcomes. Advanced statistical methods, beyond basic Punnett square analysis, are often necessary to handle these complexities.
Population Genetics and Probability
Population genetics studies the genetic variation within and between populations. Probability plays a crucial role in understanding how allele and genotype frequencies change over time.
Hardy-Weinberg Equilibrium: A Baseline for Probability in Populations
The Hardy-Weinberg principle is a cornerstone of population genetics. It states that under certain ideal conditions (no mutation, random mating, no gene flow, no genetic drift, no natural selection), allele and genotype frequencies remain constant from one generation to the next. This equilibrium provides a baseline against which to compare real-world populations and assess the impact of evolutionary forces. The Hardy-Weinberg equations use probability to predict genotype frequencies based on allele frequencies:
- p + q = 1 (where p represents the frequency of one allele and q represents the frequency of the other allele in a two-allele system)
- p² + 2pq + q² = 1 (where p² represents the frequency of homozygous dominant genotypes, 2pq represents the frequency of heterozygous genotypes, and q² represents the frequency of homozygous recessive genotypes)
These equations enable geneticists to determine whether a population is evolving or maintaining genetic equilibrium. Deviations from the Hardy-Weinberg expectations suggest that evolutionary forces are at play.
Genetic Drift and Probability: Random Fluctuations in Allele Frequencies
Genetic drift describes the random fluctuations in allele frequencies within a population, particularly pronounced in small populations. The probability of an allele becoming fixed (reaching a frequency of 100%) or lost (reaching a frequency of 0%) due to drift is directly related to its initial frequency and the population size. Computer simulations employing probabilistic models are commonly used to study the effects of genetic drift on allele frequencies over multiple generations.
Natural Selection and Probability: Differential Survival and Reproduction
Natural selection, a driving force of evolution, also has a strong probabilistic basis. Individuals with advantageous alleles are more likely to survive and reproduce, passing on their alleles to the next generation. The probability of an advantageous allele increasing in frequency depends on its selective advantage and the strength of selection. Quantitative genetics, a subfield of population genetics, employs statistical methods to model the interplay of natural selection, genetic drift, and other evolutionary forces to understand the changes in allele frequencies over time.
Genetic Counseling and Probability
Genetic counseling involves assessing the risk of genetic disorders in families and providing guidance to individuals and couples about their reproductive options. Probability plays a pivotal role in these assessments.
Pedigree Analysis and Probability: Tracing Inheritance Patterns
Pedigree analysis involves constructing family trees showing the inheritance of specific traits or disorders across multiple generations. By analyzing the inheritance pattern observed in the pedigree, genetic counselors can determine the probability of an individual inheriting a particular genotype or phenotype. This analysis often involves calculating probabilities using Bayesian methods, which update the probabilities of different scenarios as new evidence becomes available.
Risk Assessment for Genetic Disorders: Incorporating Probability and Family History
Genetic counselors use probability to estimate the risk of an individual inheriting a genetic disorder based on family history, genetic testing results, and other relevant factors. These risk assessments are crucial for informing reproductive decisions, such as whether to undergo prenatal testing or carrier screening.
Bayesian Approaches in Genetic Counseling: Updating Probabilities
Bayesian methods are particularly useful in genetic counseling because they allow for the incorporation of prior probabilities (based on population frequencies of the disorder) and likelihood ratios (based on family history and genetic testing results) to arrive at a posterior probability – a refined estimate of the risk. This iterative process allows for the continuous refinement of risk assessments as new information becomes available.
Conclusion: The Ubiquitous Role of Probability in Genetics
Probability forms the backbone of genetic analysis across diverse applications. From predicting the outcome of Mendelian crosses to understanding evolutionary processes and providing genetic counseling, probability is an indispensable tool. Understanding and applying probabilistic principles is crucial for interpreting genetic data, making informed decisions, and advancing our understanding of heredity and evolution. The advanced techniques used in genetics frequently require sophisticated statistical and probabilistic models, which continue to refine our understanding of the complexities of the genome. As our technology and understanding progress, the integration of probability will continue to be essential to the field's advancement.
Latest Posts
Latest Posts
-
An Unsaturated Fatty Acid Resulting From Hydrogenation Is Known As
Apr 04, 2025
-
What Are The Elements That Make Up Salt
Apr 04, 2025
-
Ionic Compound For Sodium And Sulfur
Apr 04, 2025
-
Cells Are Basic Unit Of Life
Apr 04, 2025
-
Two Bones That Form The Nasal Septum
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Is Probability Used In Genetics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
