How Many Atoms Are In A Simple Cubic Unit Cell
Muz Play
Apr 03, 2025 · 6 min read
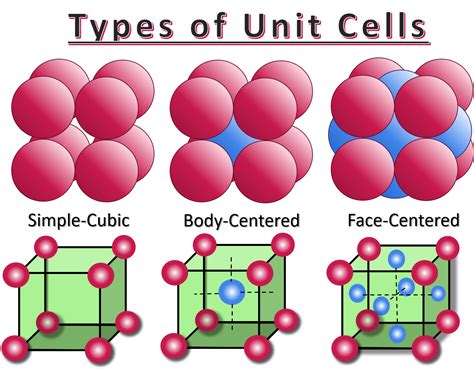
Table of Contents
How Many Atoms Are in a Simple Cubic Unit Cell? A Deep Dive into Crystallography
Understanding crystal structures is fundamental to many fields, from materials science and chemistry to physics and engineering. A crucial aspect of this understanding involves grasping the concept of the unit cell, the smallest repeating unit of a crystal lattice. This article will delve into the specifics of a simple cubic unit cell, exploring how many atoms it contains and the underlying principles governing its structure.
What is a Unit Cell?
Before focusing on the simple cubic unit cell, let's establish a firm understanding of the unit cell concept. A unit cell is the smallest repeating structural unit in a crystalline solid. Imagine a crystal as an incredibly organized three-dimensional array of atoms, ions, or molecules. The unit cell is like a building block, and by repeating this block in all three spatial directions, you can reconstruct the entire crystal structure. Different crystal structures are characterized by different unit cell geometries and the arrangement of atoms within those cells.
Several types of unit cells exist, classified primarily by their symmetry and lattice parameters. These include:
- Simple Cubic (SC): Atoms situated only at the corners of the cube.
- Body-Centered Cubic (BCC): Atoms at the corners and one atom at the center of the cube.
- Face-Centered Cubic (FCC): Atoms at the corners and one atom at the center of each of the six faces.
This article will concentrate on the simple cubic (SC) unit cell.
The Simple Cubic Unit Cell: Atom Count and Fractional Contributions
The defining characteristic of a simple cubic unit cell is the placement of atoms exclusively at the eight corners of the cube. However, it's crucial to understand that these corner atoms are shared between adjacent unit cells. A single atom located at a corner contributes only a fraction of itself to the unit cell in question.
Consider a single unit cell. Each corner atom is shared by eight adjacent unit cells. Therefore, each corner atom contributes only 1/8th of its volume to a given unit cell. Since there are eight corners in a cube, the total contribution from corner atoms to one unit cell is:
(1/8 atom/corner) * 8 corners = 1 atom
Therefore, a simple cubic unit cell contains exactly one atom.
This seemingly simple result is a cornerstone of crystallography, providing the basis for calculating atom densities, coordination numbers, and other crucial properties of crystalline materials.
Implications of the One-Atom Result: Atomic Density and Packing Efficiency
The fact that a simple cubic unit cell contains only one atom has significant implications for the material's properties. One key consequence is its relatively low atomic packing efficiency. Atomic packing efficiency refers to the percentage of the unit cell's volume that is actually occupied by atoms.
In a simple cubic structure, the atoms are arranged in a way that leaves a considerable amount of empty space. Because the atoms are only touching along the cube edges, the packing efficiency is relatively low. The atoms are not tightly packed together like in BCC or FCC structures. This results in a relatively low density for materials crystallizing in the simple cubic structure. A higher atomic packing efficiency means a denser material, often leading to enhanced strength and other mechanical properties.
Beyond the Simple Cubic: Exploring Other Unit Cell Types
While the simple cubic unit cell is conceptually straightforward, it is relatively uncommon in nature, as its low packing efficiency makes it less thermodynamically favorable compared to BCC and FCC structures. However, understanding its structure is essential for grasping the principles underlying more complex crystal lattices.
Let’s briefly touch upon the atom counts in BCC and FCC unit cells:
-
Body-Centered Cubic (BCC): A BCC unit cell has one atom at each of the eight corners (contributing 1 atom total) and one atom completely within the unit cell's body. Therefore, a BCC unit cell contains a total of two atoms.
-
Face-Centered Cubic (FCC): An FCC unit cell has one atom at each of the eight corners (contributing 1 atom total) and one atom at the center of each of the six faces. Each face-centered atom is shared by two unit cells, contributing ½ an atom to each. Thus, the contribution from the face-centered atoms is (1/2 atom/face) * 6 faces = 3 atoms. Adding the contribution from the corner atoms, an FCC unit cell contains a total of four atoms.
Relating Unit Cell Structure to Material Properties
The arrangement of atoms within the unit cell directly influences the macroscopic properties of the material. The simple cubic structure, with its low packing efficiency, often exhibits:
- Lower Density: Due to the large amount of empty space.
- Lower Hardness: The atoms are not as tightly bonded or packed, resulting in weaker interatomic interactions.
- Lower Melting Point: Weaker interatomic interactions also lead to a lower melting point.
- Higher Electrical Conductivity (in some cases): Depending on the type of atom, the arrangement could impact conductivity. However, this is heavily dependent on the specific element and its electron configuration.
The relationship between crystal structure and material properties is complex and not always straightforward. Other factors like the type of bonding, the size of the atoms, and the presence of defects also play significant roles in determining a material’s behavior.
Practical Applications and Examples of Simple Cubic Structures
While less common than BCC or FCC structures, simple cubic structures do exist in some materials under specific conditions. Examples include:
- Polonium: Under certain conditions, Polonium can crystallize in a simple cubic structure. However, it's important to note that Polonium is highly radioactive and therefore handling it requires extreme caution.
It is crucial to understand that many materials might exhibit a simple cubic structure only under specific conditions such as high temperature or pressure, and at room temperature and pressure they adopt other structures. The simple cubic structure provides a valuable foundational concept for grasping more complex structures.
Conclusion: Understanding the Fundamentals of Crystallography
Understanding the number of atoms within a simple cubic unit cell – precisely one atom – forms the bedrock of understanding crystal structures. This understanding allows us to delve into the complexities of crystallography, paving the way to predict and manipulate material properties. From the simple cubic's low packing efficiency to the contrasting densities of BCC and FCC structures, the arrangement of atoms within the unit cell profoundly impacts a material's macroscopic characteristics. This knowledge is crucial for advancements in materials science, where tailoring material properties for specific applications demands a deep understanding of crystallographic principles. Further exploration of crystal systems, including hexagonal close-packed (HCP) structures, will build upon this foundational knowledge. The simplicity of the simple cubic structure makes it an ideal entry point to understanding the fascinating world of crystallography.
Latest Posts
Latest Posts
-
Identify The Features Associated With Waxes
Apr 04, 2025
-
Rna Differs From Dna In That Rna
Apr 04, 2025
-
What Is The Net Change In Math
Apr 04, 2025
-
Why Cant The Subscripts Be Changed In A Chemical Equation
Apr 04, 2025
-
How Many Bonds Does Boron Form
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Many Atoms Are In A Simple Cubic Unit Cell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
