How To Factor Trinomials When A Is Not 1
Muz Play
Mar 29, 2025 · 5 min read
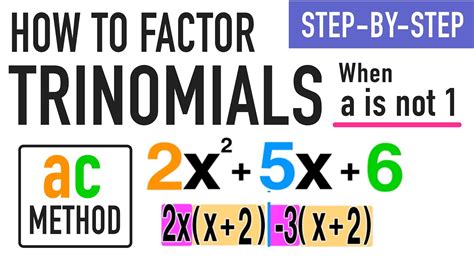
Table of Contents
How to Factor Trinomials When 'a' is Not 1
Factoring trinomials is a fundamental skill in algebra, crucial for solving quadratic equations and simplifying algebraic expressions. While factoring trinomials where the coefficient of the squared term (a) is 1 is relatively straightforward, factoring when 'a' is not 1 presents a greater challenge. This comprehensive guide will equip you with the strategies and techniques to master this important algebraic skill. We'll explore various methods, provide numerous examples, and offer tips to enhance your understanding and efficiency.
Understanding the Structure of Trinomials
Before diving into the factoring process, let's clarify the structure of a trinomial when 'a' is not 1. A general trinomial is represented as:
ax² + bx + c,
where 'a', 'b', and 'c' are constants, and 'a' ≠ 1. The goal is to express this trinomial as a product of two binomials.
Method 1: The AC Method (Product-Sum Method)
The AC method, also known as the product-sum method, is a widely used and effective technique for factoring trinomials where 'a' is not 1. Here's a step-by-step guide:
Step 1: Find the product 'ac'.
Multiply the coefficient of the squared term ('a') by the constant term ('c').
Step 2: Find two numbers that add up to 'b' and multiply to 'ac'.
This is the crucial step. You need to find two numbers whose sum is equal to the coefficient of the linear term ('b') and whose product is equal to the value you calculated in Step 1 ('ac').
Step 3: Rewrite the middle term ('bx') using the two numbers found in Step 2.
Express the middle term as the sum of two terms using the two numbers you identified.
Step 4: Factor by grouping.
Group the terms in pairs and factor out the greatest common factor (GCF) from each pair. You should then have a common binomial factor, which you can factor out.
Example:
Let's factor the trinomial 2x² + 7x + 3.
- ac = 2 * 3 = 6
- Find two numbers that add to 7 and multiply to 6. These numbers are 6 and 1 (6 + 1 = 7, 6 * 1 = 6).
- Rewrite the middle term: 2x² + 6x + 1x + 3
- Factor by grouping: 2x(x + 3) + 1(x + 3) = (2x + 1)(x + 3)
Therefore, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3).
Method 2: Trial and Error
This method involves systematically trying different combinations of binomial factors until you find the correct one. It's best suited for simpler trinomials or when you have a good intuition for factoring.
Step 1: Consider the factors of 'a'.
List the possible pairs of factors for the coefficient 'a'.
Step 2: Consider the factors of 'c'.
List the possible pairs of factors for the constant term 'c'.
Step 3: Test combinations.
Combine the factors of 'a' and 'c' in different binomial pairs, multiplying them out to check if they yield the original trinomial. This involves checking the outer and inner terms to ensure they add up to the middle term 'b'.
Example:
Let's factor 3x² + 8x + 4 using trial and error.
Possible factors of 3: (3, 1) Possible factors of 4: (4, 1), (2, 2)
Let's try (3x + 2)(x + 2): Expanding this gives 3x² + 6x + 2x + 4 = 3x² + 8x + 4. This is correct!
Therefore, the factored form of 3x² + 8x + 4 is (3x + 2)(x + 2).
Method 3: Using the Quadratic Formula (for finding roots then factoring)
While not a direct factoring method, the quadratic formula can help you find the roots of the quadratic equation ax² + bx + c = 0. These roots can then be used to write the factored form.
The quadratic formula is:
x = (-b ± √(b² - 4ac)) / 2a
Once you find the roots x₁ and x₂, the factored form is:
**a(x - x₁)(x - x₂) **
Example:
Let's use the quadratic formula to factor 2x² - 5x - 3.
a = 2, b = -5, c = -3
x = (5 ± √((-5)² - 4 * 2 * -3)) / (2 * 2) = (5 ± √49) / 4 = (5 ± 7) / 4
x₁ = 3, x₂ = -1/2
Therefore, the factored form is: 2(x - 3)(x + 1/2). To get rid of the fraction, we can multiply the whole expression by 2/2 and simplify.
2(x - 3)(x + 1/2) * 2/2 = (x - 3)(2x + 1)
Therefore, the factored form is (x - 3)(2x + 1).
Choosing the Right Method
The best method depends on the specific trinomial and your personal preference.
-
The AC method is a systematic and reliable approach that works for all trinomials. It's particularly helpful when dealing with larger numbers or when trial and error becomes cumbersome.
-
Trial and error is efficient for simpler trinomials where the factors are easily identifiable.
-
The quadratic formula is a powerful tool, especially when dealing with trinomials that are difficult to factor using the other methods or when you need to find the roots of the quadratic equation.
Advanced Techniques and Considerations
-
Factoring out a GCF First: Always check for a greatest common factor (GCF) among all the terms before applying any of the above methods. Factoring out the GCF simplifies the process and makes it easier to factor the remaining trinomial.
-
Difference of Squares: If your trinomial simplifies to a difference of squares after factoring, remember to factor it further.
-
Perfect Square Trinomials: Recognizing perfect square trinomials (of the form a² + 2ab + b² or a² - 2ab + b²) allows you to quickly factor them as (a + b)² or (a - b)².
-
Practice Makes Perfect: The more you practice factoring trinomials, the faster and more proficient you will become. Work through numerous examples, using different methods to build your skills and confidence.
Troubleshooting Common Mistakes
-
Incorrect signs: Pay close attention to the signs of the terms. Mistakes in signs are common and can lead to incorrect factored forms.
-
Errors in arithmetic: Carefully check your calculations at each step to avoid errors.
-
Forgetting to check your answer: Always expand the factored form to verify that it matches the original trinomial.
Conclusion
Factoring trinomials when 'a' is not 1 is an essential algebraic skill. By mastering the AC method, trial and error, or utilizing the quadratic formula, you'll gain confidence and proficiency in simplifying algebraic expressions and solving quadratic equations. Remember to practice regularly and pay attention to details to avoid common mistakes. With consistent effort, you'll become adept at factoring trinomials of all types. This will greatly enhance your understanding and success in higher-level mathematics.
Latest Posts
Latest Posts
-
System Of Equations With 3 Variables
Mar 31, 2025
-
Difference Between Simple Distillation And Fractional Distillation
Mar 31, 2025
-
Which Is A Major Factor Affecting Population Growth Rate
Mar 31, 2025
-
Identify The Plant Tissues In The Three Images
Mar 31, 2025
-
Thesis Statement Examples For Literary Analysis
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Factor Trinomials When A Is Not 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
