How To Find Average Acceleration From Velocity Time Graph
Muz Play
Apr 05, 2025 · 6 min read
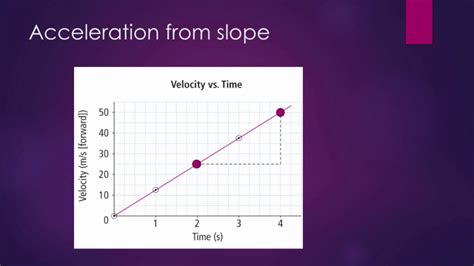
Table of Contents
How to Find Average Acceleration from a Velocity-Time Graph
Understanding acceleration is crucial in physics, and the velocity-time graph is a powerful tool for analyzing it. This comprehensive guide will walk you through everything you need to know about determining average acceleration from a velocity-time graph, covering various scenarios and providing practical examples.
What is Acceleration?
Before diving into graphs, let's clarify the concept of acceleration. Acceleration is the rate of change of velocity. This means it measures how quickly an object's velocity is changing over time. It's a vector quantity, meaning it has both magnitude (speed) and direction. A positive acceleration indicates an increase in velocity, while a negative acceleration (often called deceleration or retardation) indicates a decrease in velocity. The standard unit for acceleration is meters per second squared (m/s²).
The Velocity-Time Graph: Your Key to Understanding Acceleration
A velocity-time graph plots velocity (on the y-axis) against time (on the x-axis). The slope of the line on this graph directly represents the acceleration. This relationship forms the basis for calculating average acceleration.
Understanding the Slope: The Heart of Acceleration Calculation
- Positive Slope: A positive slope (line going upwards from left to right) indicates a positive acceleration. The object is speeding up.
- Negative Slope: A negative slope (line going downwards from left to right) indicates a negative acceleration (deceleration). The object is slowing down.
- Zero Slope: A zero slope (horizontal line) indicates zero acceleration. The object's velocity is constant; it's neither speeding up nor slowing down.
- Steeper Slope: A steeper slope indicates a larger magnitude of acceleration. The velocity is changing more rapidly.
- Shallower Slope: A shallower slope indicates a smaller magnitude of acceleration. The velocity is changing more slowly.
Calculating Average Acceleration from a Velocity-Time Graph
The average acceleration over a specific time interval can be calculated directly from the velocity-time graph using the following method:
Average Acceleration = (Change in Velocity) / (Change in Time)
Mathematically:
a<sub>avg</sub> = (v<sub>f</sub> - v<sub>i</sub>) / (t<sub>f</sub> - t<sub>i</sub>)
Where:
- a<sub>avg</sub> represents the average acceleration.
- v<sub>f</sub> represents the final velocity.
- v<sub>i</sub> represents the initial velocity.
- t<sub>f</sub> represents the final time.
- t<sub>i</sub> represents the initial time.
This formula essentially calculates the slope of the secant line connecting the two points on the velocity-time graph that correspond to the initial and final times.
Practical Examples: Deciphering Various Graph Scenarios
Let's explore various scenarios and calculate average acceleration using the velocity-time graph.
Example 1: Constant Acceleration
Imagine a car accelerating uniformly from rest (0 m/s) to 20 m/s in 5 seconds. The velocity-time graph would show a straight line with a positive slope.
To find the average acceleration:
- Identify the initial and final velocities: v<sub>i</sub> = 0 m/s, v<sub>f</sub> = 20 m/s
- Identify the initial and final times: t<sub>i</sub> = 0 s, t<sub>f</sub> = 5 s
- Apply the formula: a<sub>avg</sub> = (20 m/s - 0 m/s) / (5 s - 0 s) = 4 m/s²
The average acceleration is 4 m/s². Since the line is straight, the instantaneous acceleration at any point during this interval is also 4 m/s².
Example 2: Non-Uniform Acceleration
Consider a more realistic scenario: a car accelerating, then maintaining a constant speed, and finally braking. The velocity-time graph will show different slopes for different phases. To find the average acceleration over the entire journey, you need to determine the overall change in velocity and the total time elapsed.
Let's say:
- Initial velocity (v<sub>i</sub>) = 0 m/s
- Final velocity (v<sub>f</sub>) = 0 m/s (car comes to a stop)
- Total time elapsed (t<sub>f</sub> - t<sub>i</sub>) = 30 s
Applying the formula: a<sub>avg</sub> = (0 m/s - 0 m/s) / 30 s = 0 m/s²
Even though the car accelerated and decelerated, the average acceleration over the entire 30-second journey is 0 m/s² because the initial and final velocities are the same.
Example 3: Calculating Average Acceleration Over a Specific Interval
Suppose you want to find the average acceleration of the car only during its acceleration phase in Example 2. Let's assume the acceleration phase lasts for 10 seconds, and the car reaches a velocity of 25 m/s at the end of this phase.
- Identify the initial and final velocities for the acceleration phase: v<sub>i</sub> = 0 m/s, v<sub>f</sub> = 25 m/s
- Identify the initial and final times for the acceleration phase: t<sub>i</sub> = 0 s, t<sub>f</sub> = 10 s
- Apply the formula: a<sub>avg</sub> = (25 m/s - 0 m/s) / (10 s - 0 s) = 2.5 m/s²
The average acceleration during the acceleration phase is 2.5 m/s².
Example 4: Dealing with Negative Acceleration
Let's say a ball is thrown upwards. Its velocity decreases until it reaches its highest point (velocity = 0 m/s), then increases in the negative direction as it falls back down.
To calculate the average acceleration during its upward motion, you'd use the initial velocity (positive), the final velocity (0 m/s), and the time it takes to reach its highest point. The resulting acceleration would be negative, indicating deceleration due to gravity. Similarly, calculating the average acceleration during its downward motion would yield a positive value (still due to gravity, but considered positive since velocity is increasing in the downward (negative) direction).
Advanced Scenarios and Considerations
-
Curved Velocity-Time Graphs: For curved graphs representing non-uniform acceleration, the average acceleration is still calculated using the formula, but the calculation provides the average acceleration over the chosen interval. The instantaneous acceleration will vary at different points along the curve. Calculating instantaneous acceleration would require calculus (finding the derivative of the velocity function).
-
Units: Always ensure your units are consistent (e.g., meters per second for velocity, seconds for time).
Conclusion: Mastering the Velocity-Time Graph
The velocity-time graph is an indispensable tool for understanding and calculating acceleration. By mastering the relationship between the graph's slope and acceleration, you can confidently analyze motion in various scenarios. Remember that the average acceleration provides an overall picture of how velocity changes over a given interval, while instantaneous acceleration provides a more precise picture at any specific moment in time. By understanding these concepts, you'll have a solid foundation in kinematics and dynamics.
Latest Posts
Latest Posts
-
How Do Water Particles Move In A Wave
Apr 06, 2025
-
Why Is Density An Intensive Property
Apr 06, 2025
-
Which Of The Following Bones Belong To The Axial Skeleton
Apr 06, 2025
-
What Are The Properties Of Solids
Apr 06, 2025
-
Trends In The Periodic Table Answer Key
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How To Find Average Acceleration From Velocity Time Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
