How To Find Base Of Parallelogram
Muz Play
Apr 03, 2025 · 5 min read
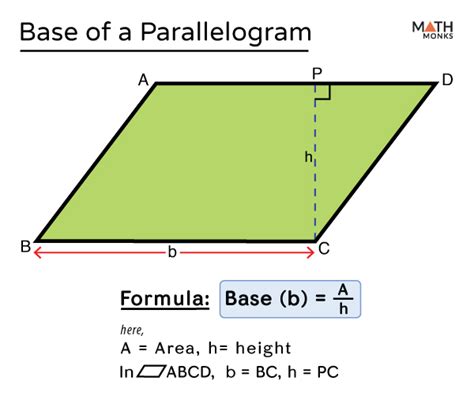
Table of Contents
How to Find the Base of a Parallelogram: A Comprehensive Guide
Finding the base of a parallelogram might seem straightforward, but understanding the nuances and different approaches is crucial for various mathematical applications. This comprehensive guide will delve into various methods to determine the base of a parallelogram, catering to different levels of mathematical understanding. We'll explore both direct calculation methods and those involving other parallelogram properties. Let's embark on this mathematical journey!
Understanding the Parallelogram and its Base
Before we delve into the methods, let's refresh our understanding of a parallelogram. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. Importantly, a parallelogram possesses several key characteristics:
- Opposite sides are parallel: This is the defining feature.
- Opposite sides are equal in length: This is a consequence of the parallel sides.
- Opposite angles are equal: The angles opposite each other are congruent.
- Consecutive angles are supplementary: The sum of any two adjacent angles is 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints.
The base of a parallelogram is simply one of its sides. While any side can be chosen as the base, it's often the side chosen for calculating the area. The height of the parallelogram is the perpendicular distance between the base and the opposite side.
Methods for Finding the Base of a Parallelogram
The method used to find the base of a parallelogram depends heavily on the information provided. Here are some common scenarios and their corresponding solution approaches:
1. Given the Area and Height
This is perhaps the most common scenario. The area of a parallelogram is given by the formula:
Area = base × height
If the area and height are known, we can easily solve for the base:
base = Area / height
Example: A parallelogram has an area of 30 square centimeters and a height of 5 centimeters. To find the base:
base = 30 cm² / 5 cm = 6 cm
Therefore, the base of the parallelogram is 6 centimeters.
2. Given the Lengths of All Sides and One Angle
In a parallelogram, opposite sides are equal. However, if you know all four sides and one angle, you can use trigonometry to find the base. Let's assume we have sides 'a' and 'b' (opposite sides are equal: a=c and b=d), and angle θ between sides 'a' and 'b'.
We can use the law of cosines to find the length of a diagonal, 'd':
d² = a² + b² - 2ab cos(θ)
Once we have the diagonal, we can use the sine rule or other trigonometric functions within the resulting triangles to find the base depending on the angle. This method involves more steps and requires a higher level of mathematical understanding.
3. Given the Coordinates of the Vertices
If the coordinates of the four vertices of the parallelogram are known, we can utilize the distance formula to find the length of each side. The distance formula between two points (x1, y1) and (x2, y2) is:
distance = √((x2 - x1)² + (y2 - y1)²)
By calculating the distances between consecutive vertices, we can determine the lengths of all four sides of the parallelogram. Remember, opposite sides will have equal lengths.
4. Given the Perimeter and the Length of One Side
The perimeter of a parallelogram is the sum of all its sides. Since opposite sides are equal in length, the formula for the perimeter (P) is:
P = 2(a + b)
Where 'a' and 'b' are the lengths of adjacent sides. If the perimeter and the length of one side are known, we can solve for the other side, which will be the base if the known side is not opposite to it.
Example: A parallelogram has a perimeter of 28 cm and one side measures 8 cm. Let's find the length of the adjacent side (base):
28 cm = 2(8 cm + b) 14 cm = 8 cm + b b = 6 cm
Therefore, the base of the parallelogram is 6 cm.
5. Using Vector Methods
For those familiar with vector algebra, the base of a parallelogram can be determined using vector operations. If we represent the sides of the parallelogram as vectors, the length of the vector representing the base gives us the base length. The vector difference between two adjacent vertices gives the vector representation of one of the sides. The magnitude of this vector is then the length of that side.
Advanced Scenarios and Considerations
While the methods above cover many common scenarios, some situations might require more advanced techniques:
- Parallelograms within complex shapes: If the parallelogram is part of a larger, more complex geometric figure, determining the base might require breaking down the problem into smaller, solvable parts.
- Parallelograms in three-dimensional space: Finding the base in 3D involves working with three coordinates for each vertex and requires vector methods or spatial geometry.
- Using properties of special parallelograms: If the parallelogram is a specific type (e.g., rhombus, rectangle, square), additional properties can simplify the calculations.
Practical Applications of Finding the Base of a Parallelogram
Understanding how to find the base of a parallelogram is essential in various fields:
- Engineering: Calculating forces, stresses, and areas in structural design.
- Physics: Determining the area of a parallelogram for vector calculations and determining the momentum of a body.
- Computer Graphics: Modeling and rendering parallelogram-shaped objects.
- Architecture: Designing and calculating areas in buildings and structures.
- Cartography: Determining areas on maps representing parallelogram-shaped land sections.
Conclusion
Finding the base of a parallelogram is a fundamental concept in geometry with practical applications in various fields. This guide has presented several methods, ranging from simple arithmetic to more advanced trigonometric and vector techniques. The optimal approach depends entirely on the available information and the mathematical tools at your disposal. Remember to carefully examine the given information and choose the most efficient method to accurately determine the base of the parallelogram. By mastering these methods, you'll enhance your problem-solving skills in geometry and related disciplines.
Latest Posts
Latest Posts
-
An Unsaturated Fatty Acid Resulting From Hydrogenation Is Known As
Apr 04, 2025
-
What Are The Elements That Make Up Salt
Apr 04, 2025
-
Ionic Compound For Sodium And Sulfur
Apr 04, 2025
-
Cells Are Basic Unit Of Life
Apr 04, 2025
-
Two Bones That Form The Nasal Septum
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find Base Of Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
