How To Find Point Of Tangency
Muz Play
Mar 29, 2025 · 6 min read
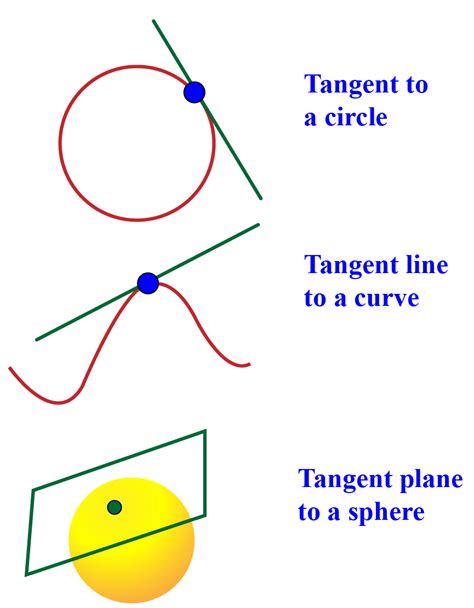
Table of Contents
How to Find the Point of Tangency: A Comprehensive Guide
Finding the point of tangency is a fundamental concept in geometry and calculus, with applications spanning various fields like physics, engineering, and computer graphics. This comprehensive guide will explore different methods for determining the point of tangency, catering to various levels of mathematical understanding. We'll delve into both geometrical and analytical approaches, equipping you with the tools to tackle diverse problems.
Understanding Tangency
Before we jump into the methods, let's clarify what we mean by "point of tangency." A tangent line is a line that touches a curve at only one point without crossing it. This single point of contact is the point of tangency. The tangent line at a specific point represents the instantaneous direction or slope of the curve at that point.
Geometrical Methods for Finding the Point of Tangency
Geometrical methods are often intuitive and visually appealing, especially when dealing with simpler curves like circles.
1. Finding the Point of Tangency for a Circle and a Line
Consider a circle with center (h, k) and radius r, and a line defined by the equation ax + by + c = 0. The point of tangency exists where the distance from the center of the circle to the line is equal to the radius.
-
Step 1: Calculate the distance from the center of the circle to the line. The formula for the distance from a point (x₁, y₁) to a line Ax + By + C = 0 is:
distance = |Ax₁ + By₁ + C| / √(A² + B²)In our case, (x₁, y₁) = (h, k), A = a, B = b, and C = c.
-
Step 2: Set the distance equal to the radius. If a tangent exists, this distance will equal the radius, r. This equation can be solved to find the coordinates of the point of tangency.
-
Step 3: Solve for the coordinates. This usually involves solving a quadratic equation. The solution(s) will represent the x and y coordinates of the point(s) of tangency. If there are two solutions, both represent points where the line is tangent to the circle.
2. Finding the Point of Tangency for Two Circles
For two circles, the point of tangency lies on the line connecting their centers.
-
Step 1: Find the equation of the line connecting the centers. Given two circles with centers (h₁, k₁) and (h₂, k₂), the equation of the line connecting the centers can be found using the two-point form of a line.
-
Step 2: Find the intersection of this line with one of the circles. Substitute the equation of the line into the equation of one of the circles. This creates a quadratic equation which, upon solving, will yield the x and y coordinates of the point(s) of intersection. If the circles are tangent, there will be only one solution.
-
Step 3: Verify tangency. Double-check that the distance between the centers is equal to the sum or difference of the radii (depending on whether the circles are externally or internally tangent).
Analytical Methods for Finding the Point of Tangency
Analytical methods leverage calculus to find points of tangency for more complex curves.
1. Using Derivatives
This method is crucial for finding the point of tangency for any differentiable curve.
-
Step 1: Find the derivative of the function. The derivative, f'(x), represents the slope of the tangent line at any point on the curve.
-
Step 2: Determine the slope of the tangent line. If you know the slope (m) of the tangent line, set f'(x) = m and solve for x. This gives you the x-coordinate of the point of tangency.
-
Step 3: Find the y-coordinate. Substitute the x-coordinate back into the original function, f(x), to obtain the corresponding y-coordinate. This completes the coordinates of the point of tangency (x, y).
-
Step 4 (optional): Write the equation of the tangent line. Using the point-slope form of a line, y - y₁ = m(x - x₁), you can write the equation of the tangent line itself.
2. Implicit Differentiation
When dealing with curves defined by implicit equations (where y isn't explicitly expressed as a function of x), we use implicit differentiation.
-
Step 1: Differentiate both sides of the equation with respect to x. Remember to use the chain rule when differentiating terms involving y.
-
Step 2: Solve for dy/dx. This gives you an expression for the slope of the tangent line at any point (x, y) on the curve.
-
Step 3: Substitute the coordinates. If you have the coordinates of a point on the curve (x₁, y₁), substitute these values into the expression for dy/dx to find the slope of the tangent line at that point.
-
Step 4: Find the equation of the tangent line (optional). Use the point-slope form of a line with the found slope and the given point (x₁, y₁).
3. Parametric Equations
If the curve is defined by parametric equations (x = f(t), y = g(t)), the approach changes slightly.
-
Step 1: Find dx/dt and dy/dt. These represent the rates of change of x and y with respect to the parameter t.
-
Step 2: Find dy/dx. The slope of the tangent line is given by dy/dx = (dy/dt) / (dx/dt).
-
Step 3: Substitute the parameter value. If you know the parameter value (t₁) at the point of tangency, substitute it into the expressions for x, y, and dy/dx to find the coordinates of the point and the slope of the tangent line.
-
Step 4: Find the equation of the tangent line (optional). Use the point-slope form of a line.
Applications of Finding the Point of Tangency
The ability to find points of tangency has wide-ranging applications:
-
Optimization Problems: Finding the maximum or minimum value of a function often involves determining the points where the tangent line is horizontal (slope = 0).
-
Physics: In kinematics, the tangent line to a position-time graph represents the instantaneous velocity.
-
Computer Graphics: Rendering smooth curves and surfaces in computer graphics relies heavily on calculating tangent lines and normals (perpendicular to the tangent).
-
Engineering: Tangent lines are used in designing curves for roads, railways, and other infrastructure to ensure smooth transitions.
Conclusion
Finding the point of tangency is a versatile skill with numerous practical applications. The methods presented here – geometrical and analytical – provide a comprehensive toolkit for handling diverse scenarios, from simple circles to complex parametric curves. Mastering these techniques will significantly enhance your understanding of geometric and calculus concepts, opening doors to problem-solving across various disciplines. Remember to carefully consider the type of curve and available information when selecting the most appropriate method. Practice is key to becoming proficient in finding the point of tangency and applying this knowledge effectively.
Latest Posts
Latest Posts
-
A Perfectly Elastic Supply Curve Is
Mar 31, 2025
-
Do Acids And Bases Conduct Electricity
Mar 31, 2025
-
Inverse Relations And Functions Quick Check
Mar 31, 2025
-
Table Salt Is A Pure Substance
Mar 31, 2025
-
What Makes Sour Patch Kids Sour
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Find Point Of Tangency . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
