How To Find The Frequency Of Oscillation
Muz Play
Mar 24, 2025 · 5 min read
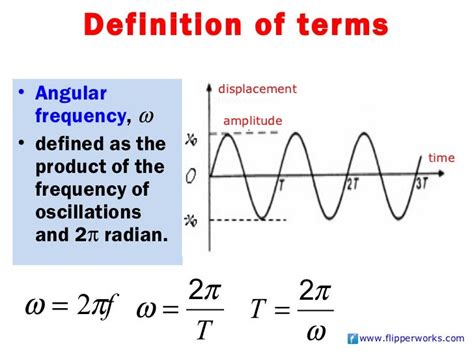
Table of Contents
- How To Find The Frequency Of Oscillation
- Table of Contents
- How to Find the Frequency of Oscillation: A Comprehensive Guide
- Understanding Frequency and its Units
- Methods for Determining Oscillation Frequency
- 1. Direct Measurement using a Timer or Oscilloscope:
- 2. Analytical Methods for Simple Harmonic Motion (SHM):
- 3. Fourier Analysis for Complex Oscillations:
- 4. Resonance Phenomena:
- 5. Spectral Analysis:
- Practical Considerations and Error Analysis:
- Examples Across Disciplines:
- Conclusion:
- Latest Posts
- Latest Posts
- Related Post
How to Find the Frequency of Oscillation: A Comprehensive Guide
Oscillation, the repetitive variation, typically in time, of some measure about a central value (often a point of equilibrium) is a fundamental concept across numerous scientific disciplines. Understanding how to determine the frequency of this oscillation – the number of oscillations per unit of time – is crucial for analyzing various systems, from simple pendulums to complex electrical circuits. This comprehensive guide delves into various methods for finding the frequency of oscillation, catering to different levels of understanding and system complexities.
Understanding Frequency and its Units
Before we dive into the methods, let's clarify the concept of frequency. Frequency (f) is defined as the number of complete cycles or oscillations that occur per unit of time. The standard unit for frequency is Hertz (Hz), representing one cycle per second. Other units, such as kilohertz (kHz, 1000 Hz), megahertz (MHz, 1,000,000 Hz), and gigahertz (GHz, 1,000,000,000 Hz), are used for higher frequencies. The inverse of frequency is the period (T), which represents the time it takes for one complete oscillation. Therefore, the relationship between frequency and period is:
f = 1/T or T = 1/f
Methods for Determining Oscillation Frequency
The method used to determine the frequency of oscillation depends heavily on the type of oscillating system. We'll explore several common approaches:
1. Direct Measurement using a Timer or Oscilloscope:
This is the most straightforward method, especially for systems with easily observable oscillations.
-
Simple Pendulum or Mass-Spring System: For a simple pendulum or mass-spring system exhibiting visible oscillations, you can use a stopwatch to measure the time taken for a specific number of oscillations (e.g., 10 or 20). Divide the total time by the number of oscillations to obtain the period (T). Then, calculate the frequency using the formula f = 1/T. This method relies on accurate timing, and human error can introduce some uncertainty.
-
Oscilloscope: For higher frequency oscillations or those that are too rapid for manual timing, an oscilloscope is invaluable. An oscilloscope displays the waveform of the oscillation, allowing you to measure the period directly from the screen. The horizontal axis represents time, and you can measure the time for one complete cycle. Again, frequency is calculated using f = 1/T. Oscilloscopes offer significantly higher precision than manual timing.
2. Analytical Methods for Simple Harmonic Motion (SHM):
Many oscillating systems, under certain conditions, exhibit simple harmonic motion (SHM). SHM is characterized by a sinusoidal waveform and a restoring force proportional to the displacement from equilibrium. For such systems, the frequency can be determined analytically.
- Simple Pendulum: The frequency of a simple pendulum (a mass suspended from a string of negligible mass) is given by:
f = 1/(2π)√(g/L)
Where:
- g is the acceleration due to gravity (approximately 9.81 m/s² on Earth).
- L is the length of the pendulum.
This formula highlights the inverse relationship between frequency and pendulum length; longer pendulums oscillate at lower frequencies.
- Mass-Spring System: The frequency of oscillation for a mass-spring system is given by:
f = 1/(2π)√(k/m)
Where:
- k is the spring constant (a measure of the spring's stiffness).
- m is the mass attached to the spring.
This equation shows that stiffer springs (higher k) result in higher frequencies, while larger masses (higher m) lead to lower frequencies.
3. Fourier Analysis for Complex Oscillations:
Many real-world oscillations are not simple sinusoidal waves. They might be composed of multiple frequencies superimposed. Fourier analysis is a powerful mathematical technique used to decompose a complex waveform into its constituent sinusoidal components, revealing the individual frequencies present. This technique is extensively used in signal processing and various fields of engineering. Software packages and specialized instruments can perform Fourier transforms efficiently.
4. Resonance Phenomena:
The phenomenon of resonance can be exploited to determine the natural frequency of an oscillating system. A system subjected to an external periodic force will vibrate with maximum amplitude when the driving frequency matches its natural frequency. By carefully observing the amplitude of oscillations while varying the driving frequency, one can identify the resonance frequency, which is equivalent to the natural frequency of the system.
5. Spectral Analysis:
Spectral analysis techniques, closely related to Fourier analysis, analyze the frequency components present in a signal. These techniques are used in various scientific and engineering fields, like acoustics, seismology, and radio astronomy. Specialized software and instruments are employed to perform spectral analysis, which can reveal a detailed frequency spectrum of a complex oscillation.
Practical Considerations and Error Analysis:
When determining the frequency of oscillation, several practical factors must be considered:
-
Measurement Errors: Inherent errors exist in any measurement. Carefully assessing these errors and reporting them with the results is crucial for scientific rigor. Human error in timing, instrument limitations, and environmental factors can contribute to measurement uncertainty.
-
Damping Effects: Real-world oscillating systems are subject to damping forces (friction, air resistance, etc.) that gradually reduce the amplitude of oscillations. Damping can affect the measured frequency, especially in strongly damped systems. For accurate measurements, minimize damping effects as much as possible.
-
Non-linearity: The analytical methods described above are valid primarily for linear systems where the restoring force is directly proportional to the displacement. Non-linear systems may exhibit more complex oscillations with frequencies that depend on the amplitude of oscillation. In such cases, advanced analytical or numerical techniques are often required.
Examples Across Disciplines:
The determination of oscillation frequency finds applications in numerous fields:
- Physics: Analyzing the oscillations of pendulums, springs, and LC circuits.
- Engineering: Designing structures to withstand vibrations, controlling oscillations in mechanical systems.
- Electronics: Analyzing the frequency response of circuits, tuning oscillators to precise frequencies.
- Acoustics: Determining the pitch and timbre of musical instruments and sounds.
- Seismology: Analyzing seismic waves to understand earthquakes.
- Medical Imaging: Employing techniques like ultrasound and MRI, which rely on the principles of oscillations.
Conclusion:
Finding the frequency of oscillation involves a range of techniques, from simple direct measurements to sophisticated analytical and spectral analysis methods. The appropriate method depends heavily on the type of oscillating system, its complexity, and the desired accuracy. Understanding the underlying principles of oscillation and applying appropriate measurement and analysis techniques are crucial for accurate results and meaningful interpretations across diverse scientific and engineering disciplines. Careful consideration of potential errors and the limitations of each technique is also essential for achieving reliable and robust findings.
Latest Posts
Latest Posts
-
Movement Of Particles From High To Low Concentration
Mar 29, 2025
-
Nucleic Acids Are Made Of Monomers Called
Mar 29, 2025
-
1 2 Addition Vs 1 4 Addition
Mar 29, 2025
-
Why Is A Cell The Basic Unit Of Life
Mar 29, 2025
-
Example Of Gas Dissolved In Gas
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Frequency Of Oscillation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
