Inscribed Circle In A Right Triangle
Muz Play
Apr 02, 2025 · 5 min read
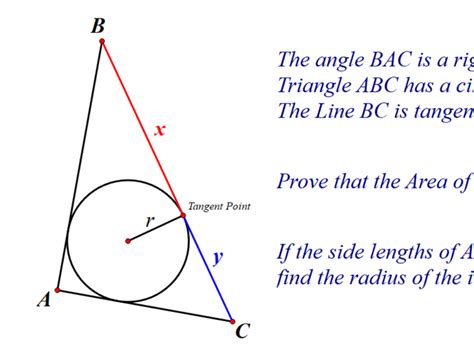
Table of Contents
- Inscribed Circle In A Right Triangle
- Table of Contents
- Inscribed Circle in a Right Triangle: A Comprehensive Guide
- Understanding the Incenter and its Significance
- Calculating the Radius of the Inscribed Circle in a Right Triangle
- Deriving the Formula: A Step-by-Step Approach
- Exploring the Relationship between the Inradius and the Triangle's Sides
- The Area of the Inscribed Circle: A Simple Calculation
- Applications and Problem-Solving: Real-World Examples
- Advanced Concepts and Further Exploration
- Conclusion: Mastering the Inscribed Circle
- Latest Posts
- Latest Posts
- Related Post
Inscribed Circle in a Right Triangle: A Comprehensive Guide
The inscribed circle, or incircle, of a triangle is the largest circle that can be contained within the triangle; it touches each of the triangle's three sides. Understanding the properties of an inscribed circle, especially within the context of a right-angled triangle, opens doors to fascinating geometric relationships and problem-solving techniques. This comprehensive guide will delve into the intricacies of the incircle in a right triangle, exploring its radius, area, and connections to other triangle elements.
Understanding the Incenter and its Significance
Before diving into the specifics of a right-angled triangle, let's establish a fundamental concept: the incenter. The incenter is the point where the three angle bisectors of a triangle intersect. This point is equidistant from all three sides of the triangle, and this distance is the radius (r) of the inscribed circle. The incenter is crucial because it defines the center of the incircle, dictating its position within the triangle.
In a right-angled triangle, the incenter's location takes on a unique characteristic. Due to the properties of angle bisectors, the incenter always lies within the triangle, never outside it.
Calculating the Radius of the Inscribed Circle in a Right Triangle
The radius of the incircle (r) in any triangle can be calculated using the formula: Area = rs, where 'Area' represents the area of the triangle, and 's' represents the semi-perimeter (half the perimeter). For a right-angled triangle with sides a, b, and hypotenuse c, the formula simplifies beautifully.
Deriving the Formula: A Step-by-Step Approach
-
Area Calculation: The area of a right-angled triangle is simply (1/2)ab, where 'a' and 'b' are the legs of the right triangle.
-
Semi-perimeter Calculation: The semi-perimeter (s) is calculated as s = (a + b + c) / 2.
-
Substituting into the General Formula: Substituting the area and semi-perimeter into the general formula (Area = rs), we get: (1/2)ab = r[(a + b + c) / 2].
-
Simplifying to Solve for r: This simplifies to: r = ab / (a + b + c). This elegant formula allows us to directly compute the radius of the incircle in a right-angled triangle using only the lengths of its sides.
Exploring the Relationship between the Inradius and the Triangle's Sides
The formula r = ab / (a + b + c) reveals a powerful relationship between the incircle's radius and the lengths of the triangle's sides. Notice that the radius is directly proportional to the product of the legs (ab) and inversely proportional to the perimeter (a + b + c). This means:
- Larger legs, larger radius: If the legs of the right triangle are longer, the radius of the incircle will be larger.
- Larger perimeter, smaller radius: If the perimeter of the triangle increases, the radius of the incircle will decrease. This makes intuitive sense; a larger triangle will tend to have a smaller relative incircle.
This relationship is fundamental in solving problems involving the incircle and the dimensions of the right triangle.
The Area of the Inscribed Circle: A Simple Calculation
Once the radius (r) is known, calculating the area of the incircle is straightforward. The area of a circle is given by the formula Area = πr². Therefore, by substituting the calculated value of 'r', we can easily find the area of the incircle within the right-angled triangle.
This seemingly simple calculation becomes a powerful tool when combined with other geometric properties of the right triangle, allowing for elegant solutions to complex problems.
Applications and Problem-Solving: Real-World Examples
The concept of the inscribed circle in a right triangle finds numerous applications in various fields, including:
- Engineering and Design: Calculating the maximum size of a circular component that can fit inside a right-angled structural element.
- Architecture and Construction: Determining the size of a circular feature within a right-angled building design.
- Computer Graphics and Game Development: Creating realistic geometric representations and simulations.
- Mathematics Competitions and Puzzles: Posing and solving intriguing geometric problems that test understanding of these principles.
Let's explore a few examples to solidify our understanding:
Example 1: A right-angled triangle has legs of length 6 cm and 8 cm. Calculate the radius of its inscribed circle.
-
Calculate the hypotenuse: Using the Pythagorean theorem (c² = a² + b²), we get c = √(6² + 8²) = 10 cm.
-
Calculate the semi-perimeter: s = (6 + 8 + 10) / 2 = 12 cm.
-
Calculate the area: Area = (1/2) * 6 * 8 = 24 cm².
-
Use the formula Area = rs: 24 = r * 12, therefore r = 2 cm.
Example 2: A right triangle has an incircle with a radius of 3 cm. One leg is twice the length of the other. Find the lengths of the sides.
This problem requires a slightly different approach. We'll use the formula r = ab/(a+b+c) and the relationship between the legs. Let's assume one leg is 'x' and the other is '2x'. The hypotenuse will be √(x² + (2x)²). Substituting into the radius formula and solving for x will yield the lengths of the sides. This type of problem demonstrates the power of combining algebraic manipulation with geometric principles.
Advanced Concepts and Further Exploration
The study of incircles in right-angled triangles extends beyond basic calculations. More advanced concepts include:
- Relationship with Excircles: A triangle also possesses excircles (circles tangent to one side and the extensions of the other two sides). Exploring the relationships between the incircle and excircles offers deeper insight into the triangle's geometry.
- Euler's Theorem: This theorem connects the distance between the incenter and circumcenter (the center of the circle passing through the triangle's vertices) to the radii of the incircle and circumcircle.
- Tangency Points: The points where the incircle touches the sides of the triangle are significant; investigating their properties and relationships can lead to interesting geometric deductions.
Conclusion: Mastering the Inscribed Circle
Understanding the inscribed circle in a right-angled triangle is more than just memorizing formulas; it's about grasping the underlying geometric relationships and leveraging these principles to solve problems creatively. By mastering the concepts presented here, you gain a deeper appreciation for the beauty and elegance of geometry, opening up new avenues for exploration and problem-solving in various mathematical and practical contexts. From simple radius calculations to more advanced explorations, the inscribed circle remains a fascinating subject with enduring relevance in mathematics and beyond.
Latest Posts
Latest Posts
-
Family As An Agent Of Socialisation
Apr 05, 2025
-
Does Proton And Neutron Have The Same Mass
Apr 05, 2025
-
Water Has High Heat Of Vaporization
Apr 05, 2025
-
Find The Tangent Plane To The Surface At The Point
Apr 05, 2025
-
What Are The Characteristics Of A Covalent Bond
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Inscribed Circle In A Right Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
