Magnetic Field For A Circular Loop
Muz Play
Mar 27, 2025 · 7 min read
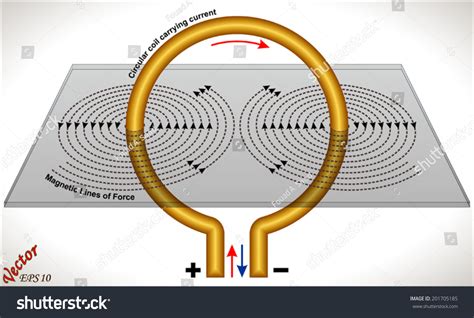
Table of Contents
Magnetic Field of a Circular Loop: A Comprehensive Guide
The magnetic field generated by a current-carrying circular loop is a fundamental concept in electromagnetism with widespread applications in various technologies, from electric motors to MRI machines. Understanding its characteristics, calculation, and implications is crucial for anyone studying physics, engineering, or related fields. This comprehensive guide delves into the intricacies of the magnetic field produced by a circular loop, providing a detailed explanation suitable for both beginners and advanced learners.
Understanding the Basics: Current, Loops, and Magnetic Fields
Before diving into the specifics of a circular loop, let's establish a foundational understanding. A magnetic field is a vector field that surrounds a moving charge or a current-carrying conductor. This field exerts a force on other moving charges and magnets. The strength and direction of this force depend on the magnitude and direction of the magnetic field, as well as the charge and velocity of the moving particle.
A current, represented by the symbol I, is the flow of electric charge. In a wire, this charge flow is typically due to the movement of electrons. The magnitude of the current is measured in Amperes (A).
When we arrange a current-carrying wire into a loop, the magnetic fields produced by each segment of the wire interact. This interaction leads to a characteristic magnetic field pattern, significantly different from that of a straight wire. The shape of the loop influences the overall magnetic field. A circular loop, due to its symmetry, creates a particularly interesting and important field configuration.
Calculating the Magnetic Field at the Center of a Circular Loop
The simplest case to analyze is the magnetic field at the center of the loop. Using the Biot-Savart law, a powerful tool for calculating magnetic fields generated by current distributions, we can determine the field strength. The Biot-Savart law states that the magnetic field dB produced by a small current element Idl is proportional to the current, the length of the element, and inversely proportional to the square of the distance from the element:
dB = (μ₀/4π) * (Idl x r) / r³
where:
- dB is the magnetic field produced by the current element
- μ₀ is the permeability of free space (4π x 10⁻⁷ T·m/A)
- I is the current in the loop
- dl is a small vector element of the loop, tangent to the loop and in the direction of the current
- r is the vector from the current element to the point where the field is being calculated (the center of the loop in this case)
- x denotes the cross product
For a circular loop of radius R, the integration of the Biot-Savart law over the entire loop simplifies significantly due to the symmetry. Each small element dl contributes a magnetic field element dB that points perpendicular to the plane of the loop. The integration essentially sums up all these contributions. The result of this integration provides the magnitude of the magnetic field at the center of the loop:
B = (μ₀I) / (2R)
This equation reveals that the magnetic field at the center is directly proportional to the current and inversely proportional to the radius of the loop. This means a larger current produces a stronger field, while a larger loop radius produces a weaker field.
Vector Nature of the Magnetic Field
It's crucial to remember that the magnetic field is a vector quantity, meaning it has both magnitude and direction. At the center of the loop, the direction of the magnetic field is perpendicular to the plane of the loop. Using the right-hand rule, if you curl the fingers of your right hand in the direction of the current, your thumb will point in the direction of the magnetic field.
Magnetic Field at Points on the Axis of a Circular Loop
Determining the magnetic field at points along the axis of the loop (i.e., the line perpendicular to the plane of the loop and passing through its center) requires a more complex integration. While the symmetry simplifies the problem compared to arbitrary points in space, we still need to consider the varying distances and angles between the current elements and the point of interest.
Using the Biot-Savart law and integrating over the loop, we arrive at the following expression for the magnetic field at a point on the axis of the loop a distance z from the center:
B = (μ₀IR²) / (2(R² + z²)^(3/2))
This equation shows that the field strength decreases as the distance z from the center increases. The field is strongest at the center (z=0) and diminishes as we move along the axis. This behavior is consistent with the inverse square law behavior of many other physical phenomena.
Analyzing the Axial Field
This formula reveals several important characteristics of the axial magnetic field:
- Maximum Field: The magnetic field is maximum at the center of the loop (z = 0), as shown earlier.
- Symmetry: The field is symmetric about the plane of the loop. The magnitude of the field is the same at equal distances above and below the plane.
- Asymptotic Behavior: As the distance z becomes very large compared to the radius R, the magnetic field weakens rapidly, approaching zero. This is expected as the loop appears smaller and smaller from far away.
Magnetic Field at Points Off-Axis: A Complex Calculation
Calculating the magnetic field at points off the axis of a circular loop is significantly more complex. The symmetry that simplified the on-axis and center calculations is lost. This requires integrating the Biot-Savart law over the loop with more intricate geometry considerations. The resulting expression is not a simple, closed-form equation. Instead, it typically involves elliptic integrals, which are special mathematical functions. These integrals often require numerical methods for evaluation.
While a precise analytical solution is mathematically challenging, several approximation methods can be employed depending on the specific location and the relative sizes of the loop radius and the distance from the loop.
Applications of Circular Loop Magnetic Fields
The magnetic field of a circular loop has numerous practical applications across various scientific and technological fields. Some noteworthy examples include:
1. Electromagnets:
Circular loops are fundamental components of electromagnets. By passing a current through a coil (multiple circular loops wound together), a strong and controllable magnetic field is generated. The strength of the field can be adjusted by changing the current or the number of loops. Electromagnets are used extensively in various applications, including motors, generators, and magnetic levitation systems.
2. Magnetic Resonance Imaging (MRI):
MRI machines rely on strong, precisely controlled magnetic fields to generate detailed images of the human body. These fields are often created using a combination of large superconducting coils, including circular loops, arranged in sophisticated configurations. The strength and homogeneity of these fields are crucial for obtaining high-quality images.
3. Particle Accelerators:
Circular loops of wire, often arranged in large rings, are used in particle accelerators to guide and accelerate charged particles. These loops generate magnetic fields that bend the paths of the particles, keeping them confined within the accelerator structure while simultaneously increasing their energy.
4. Sensors:
Circular loops can be used as sensors to detect the presence and strength of magnetic fields. Changes in the magnetic field induce currents in the loop, which can be measured to determine the properties of the external field. This principle underlies many types of magnetic field sensors.
5. Wireless Power Transfer:
Inductive coupling, which utilizes the magnetic fields generated by circular loops, is employed in wireless power transfer systems. One loop generates a magnetic field that induces a current in a nearby receiving loop, transferring energy without physical contact. This technology is increasingly used for charging portable devices and powering implantable medical devices.
Conclusion: The Significance of Circular Loop Magnetic Fields
The magnetic field produced by a current-carrying circular loop is a cornerstone concept in electromagnetism. Its relatively simple geometry, yet rich mathematical description, provides a fertile ground for understanding fundamental principles and exploring advanced applications. From calculating the field strength at various points to understanding the practical applications of this field, this comprehensive guide has explored the nuances and significance of this essential concept in electromagnetism, laying the groundwork for further exploration in the field. The continued study and refinement of our understanding of these fields will undoubtedly lead to further technological advancements in various sectors.
Latest Posts
Latest Posts
-
Formula For Area Of Cross Section
Mar 30, 2025
-
What Type Of Ion Will Calcium Form
Mar 30, 2025
-
The Atomic Mass Number Is Equal To
Mar 30, 2025
-
Where Does Dna Replication Take Place In A Eukaryotic Cell
Mar 30, 2025
-
Find Standard Matrix Of Linear Transformation
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Magnetic Field For A Circular Loop . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
