Moment Of Inertia Of A Point
Muz Play
Apr 01, 2025 · 6 min read
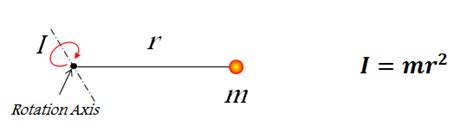
Table of Contents
Moment of Inertia of a Point Mass: A Deep Dive
The concept of moment of inertia is fundamental in physics, particularly in mechanics and rotational dynamics. It quantifies an object's resistance to changes in its rotation. While often applied to extended bodies, understanding the moment of inertia of a point mass is crucial for building a solid foundation. This article provides a comprehensive exploration of this concept, covering its definition, calculation, significance, and applications.
Understanding Moment of Inertia
Moment of inertia, often denoted as I, isn't simply a measure of mass; it's a measure of how that mass is distributed relative to an axis of rotation. For a point mass, this distribution is straightforward. Imagine a tiny particle of mass m located at a distance r from an axis of rotation. The moment of inertia of this point mass about that axis is simply:
I = mr²
This simple equation encapsulates the essence of moment of inertia:
-
Mass (m): A larger mass resists changes in rotation more strongly. Think of a heavier spinning top versus a lighter one – the heavier one is harder to stop or speed up.
-
Distance from the axis of rotation (r): The further the mass is from the axis, the greater its contribution to the overall moment of inertia. This is why it's harder to spin a long, slender rod compared to a short, thick one, even if they have the same mass. The mass is distributed further from the axis in the slender rod.
Deriving the Formula: A Mathematical Perspective
While the formula I = mr² is presented as a straightforward fact, its derivation provides valuable insight into the physics behind moment of inertia. The derivation involves considering the kinetic energy of rotation.
The kinetic energy of a point mass moving linearly with velocity v is given by:
KE = ½mv²
When this point mass is rotating about an axis at a distance r with angular velocity ω, its linear velocity is related to the angular velocity by:
v = ωr
Substituting this into the kinetic energy equation, we get:
KE = ½m(ωr)² = ½mr²ω²
Now, observe that the term mr² is independent of the angular velocity. We define this term as the moment of inertia, I:
I = mr²
Therefore, the kinetic energy of rotation can be expressed more concisely as:
KE = ½Iω²
This equation is analogous to the linear kinetic energy equation (KE = ½mv²) and highlights the parallel between linear and rotational motion. The moment of inertia plays the role analogous to mass in rotational dynamics.
Moment of Inertia vs. Mass: Key Differences
It's crucial to distinguish between moment of inertia and mass. While mass is a scalar quantity representing the amount of matter in an object, moment of inertia is a tensor quantity (although for a point mass, it simplifies to a scalar). It depends not only on the mass but also on its distribution relative to the axis of rotation.
| Feature | Mass | Moment of Inertia |
|---|---|---|
| Definition | Amount of matter | Resistance to rotational acceleration |
| Type | Scalar | Tensor (scalar for point mass) |
| Dependence | Independent of location/orientation | Dependent on mass distribution and rotation axis |
| Units | kg | kg·m² |
Calculating Moment of Inertia for Different Axes
For a point mass, the moment of inertia is simple: I = mr². However, the choice of the axis of rotation is crucial. If the axis of rotation passes through the point mass, then r = 0, and the moment of inertia is zero. This makes intuitive sense; a point mass rotating about itself experiences no resistance to change in its rotation.
If the axis of rotation is parallel to a certain direction and passes through a point at distance d from the point mass, then the parallel axis theorem can be used to determine the moment of inertia. The parallel axis theorem states that:
I = I_cm + md²
where I_cm is the moment of inertia about an axis through the center of mass (which is the point mass itself in this case, so I_cm = 0) and d is the distance between the two parallel axes.
Therefore, the moment of inertia about this parallel axis is simply:
I = md²
Applications of Moment of Inertia of a Point Mass
While seemingly simple, the concept of the moment of inertia of a point mass has wide-ranging applications:
-
Building blocks for complex systems: The moment of inertia of extended bodies is often calculated by integrating the contributions of infinitesimal point masses throughout the object. The simple formula for a point mass serves as the foundation for these more complex calculations.
-
Rotational kinetic energy: As shown earlier, the moment of inertia is crucial for determining the rotational kinetic energy of a rotating system. Understanding this allows us to analyze the energy transfer in various scenarios, such as spinning wheels, rotating machinery, and celestial bodies.
-
Angular momentum: Angular momentum, a crucial concept in physics, is closely related to the moment of inertia. For a point mass, the angular momentum (L) is given by:
L = Iω = mr²ω
-
Simple Harmonic Motion (SHM): The concept of moment of inertia is crucial in the analysis of the torsional oscillations of a physical pendulum or a system exhibiting rotational SHM. The moment of inertia determines the period of oscillation.
The Parallel Axis Theorem: Extending the Concept
The parallel axis theorem allows us to calculate the moment of inertia of a point mass about an axis parallel to an axis passing through the point mass itself. This is a vital tool when dealing with more complex systems composed of multiple point masses or extended bodies.
The Perpendicular Axis Theorem: Two-Dimensional Systems
The perpendicular axis theorem is applicable for planar objects (two-dimensional). For a point mass lying in a plane, if I_x and I_y are the moments of inertia about two perpendicular axes in the plane, and I_z is the moment of inertia about an axis perpendicular to the plane passing through the point of intersection of x and y axes, then:
I_z = I_x + I_y
This theorem simplifies calculations for planar systems.
Moment of Inertia and Radius of Gyration
The radius of gyration (k) provides a measure of how far from the axis of rotation the mass of a body is effectively concentrated. For a point mass, the radius of gyration is simply:
k = √(I/m) = r
Conclusion: A Fundamental Concept in Rotational Dynamics
The moment of inertia of a point mass, while seemingly a simple concept, underpins the understanding of rotational motion. Its application extends far beyond the point mass itself, serving as a building block for analyzing complex rotational systems in various fields of physics and engineering. Mastering this fundamental concept is crucial for anyone seeking a deeper understanding of rotational dynamics and its myriad applications in the world around us. From the design of rotating machinery to the study of celestial mechanics, the seemingly simple formula I = mr² holds significant weight in the realm of physics. Further exploration into the parallel and perpendicular axis theorems, along with the concept of radius of gyration, provides a complete picture of this critical element in rotational mechanics.
Latest Posts
Latest Posts
-
Base Excision Repair Vs Mismatch Repair
Apr 02, 2025
-
Is Argon Metal Nonmetal Or Metalloid
Apr 02, 2025
-
What Is A Limiting Amino Acid In A Protein
Apr 02, 2025
-
Under What Conditions Are Gases Most Likely To Behave Ideally
Apr 02, 2025
-
How To Find The Vertical Asymptote Of A Limit
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of A Point . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
