Newton's Second Law In Rotational Form
Muz Play
Apr 05, 2025 · 6 min read
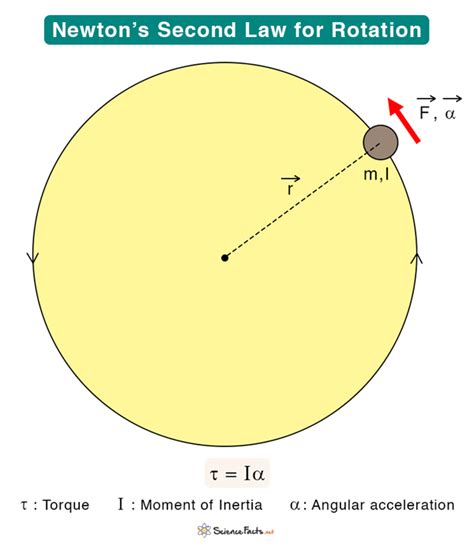
Table of Contents
Newton's Second Law in Rotational Form: A Deep Dive
Newton's second law, famously expressed as F=ma (force equals mass times acceleration), is a cornerstone of classical mechanics. It elegantly describes the relationship between force and linear motion. However, much of the world doesn't move in straight lines; it rotates. Understanding motion involving rotation requires extending Newton's second law into its rotational equivalent. This article will delve deep into Newton's second law in rotational form, exploring its derivation, applications, and significance in various physical phenomena.
From Linear to Rotational: Understanding the Analogy
Before diving into the intricacies of the rotational form, let's establish the fundamental analogy between linear and rotational motion. Many quantities have rotational counterparts:
| Linear Quantity | Symbol | Rotational Counterpart | Symbol | Relationship |
|---|---|---|---|---|
| Displacement | x | Angular Displacement | θ (theta) | x = rθ (r = radius) |
| Velocity | v | Angular Velocity | ω (omega) | v = rω |
| Acceleration | a | Angular Acceleration | α (alpha) | a = rα |
| Mass | m | Moment of Inertia | I | Depends on mass distribution |
| Force | F | Torque | τ (tau) | τ = rFsin(φ) (φ = angle between r and F) |
| Momentum | p | Angular Momentum | L | L = Iω |
This table highlights the crucial parallel between linear and rotational quantities. Notice that the radius, 'r', plays a pivotal role in connecting linear and rotational parameters. Understanding these analogies is crucial to grasping Newton's second law in its rotational form.
Deriving Newton's Second Law for Rotation
Newton's second law states that the net force acting on an object is equal to the product of its mass and its acceleration: ΣF = ma. To derive the rotational equivalent, consider a single particle of mass 'm' rotating about a fixed axis at a distance 'r' with an angular acceleration 'α'.
The tangential acceleration (a<sub>t</sub>) of this particle is related to its angular acceleration by a<sub>t</sub> = rα. The net tangential force (ΣF<sub>t</sub>) acting on the particle is given by Newton's second law: ΣF<sub>t</sub> = ma<sub>t</sub> = mrα.
The torque (τ) exerted on the particle is the product of the tangential force and the radius: τ = rΣF<sub>t</sub> = r(mrα) = mr²α.
For a rigid body composed of many particles, the total torque is the sum of the torques acting on each particle:
Στ = Σ(mr²α) = α Σ(mr²)
The term Σ(mr²) represents the moment of inertia (I) of the rigid body, which depends on the mass distribution and the axis of rotation. Therefore, we arrive at the rotational analogue of Newton's second law:
Στ = Iα
This equation states that the net torque acting on a rigid body is equal to the product of its moment of inertia and its angular acceleration. This is the fundamental equation governing rotational dynamics.
Understanding Moment of Inertia: The Rotational Mass
The moment of inertia (I) is the rotational equivalent of mass in linear motion. It quantifies the resistance of a body to changes in its rotational motion. Unlike mass, which is a scalar quantity, the moment of inertia is a tensor, meaning its value depends on the axis of rotation.
Calculating the moment of inertia involves summing the product of each particle's mass and the square of its distance from the axis of rotation. For continuous bodies, integration is necessary:
I = ∫r²dm
The moment of inertia depends heavily on the shape and mass distribution of the object. Simple objects have well-defined formulas for their moment of inertia:
- Solid cylinder or disk: I = (1/2)MR²
- Solid sphere: I = (2/5)MR²
- Hollow cylinder or ring: I = MR²
- Rod about its center: I = (1/12)ML²
- Rod about its end: I = (1/3)ML²
Where M is the total mass and R or L is the relevant radius or length. These formulas are crucial for applying Newton's second law in rotational form to various scenarios.
Applications of Newton's Second Law in Rotational Form
The applications of Newton's second law in rotational form are vast and span numerous fields of physics and engineering. Here are some key examples:
1. Rotational Dynamics of Rigid Bodies:
This forms the basis for understanding the motion of rotating objects like wheels, gears, gyroscopes, and spinning tops. Analyzing their acceleration, velocity, and stability requires a thorough understanding of the rotational form of Newton's second law.
2. Pulley Systems and Atwood Machines:
Analyzing the motion of masses connected by a pulley system involves applying both linear and rotational forms of Newton's second law. The tension in the rope and the angular acceleration of the pulley can be determined by considering the torques and forces involved.
3. Rolling Motion:
Rolling motion combines both translational and rotational motion. Applying Newton's second law in both linear and rotational forms allows for a complete description of the object's motion, including its acceleration and velocity. This is crucial in analyzing the motion of vehicles, balls, and other rolling objects.
4. Angular Momentum Conservation:
In the absence of external torques, the angular momentum of a system remains constant. This principle, derived from Newton's second law in rotational form, plays a vital role in understanding phenomena like the spinning of ice skaters or the stability of satellites.
5. Gyroscopic Motion:
Gyroscopes exhibit remarkable stability due to the conservation of angular momentum. Understanding their precession and nutation necessitates the application of Newton's second law in its rotational form, coupled with concepts of torque and angular momentum.
Advanced Concepts and Considerations
While the basic form Στ = Iα provides a good foundation, more advanced considerations are needed for complex systems:
-
Non-constant Moment of Inertia: For objects with varying mass distribution or flexible bodies, the moment of inertia might change during rotation. This requires more sophisticated analysis techniques.
-
Parallel Axis Theorem: This theorem allows calculating the moment of inertia about any axis parallel to an axis through the center of mass. This is useful when the axis of rotation isn't directly through the center of mass.
-
Perpendicular Axis Theorem: This theorem is applicable to planar objects and simplifies moment of inertia calculations for axes perpendicular to the plane.
Conclusion: The Power of Rotational Dynamics
Newton's second law in rotational form, Στ = Iα, is a powerful tool for understanding the dynamics of rotating systems. By connecting linear and rotational quantities through the moment of inertia and torque, this equation provides a unified framework for analyzing a vast range of physical phenomena. From the simple spinning of a top to the complex motion of planets and satellites, this law illuminates the intricate workings of our rotating universe. Its applications are widespread in engineering, physics, and other scientific disciplines, making its study crucial for anyone seeking a deeper understanding of the world around us. The deeper you delve into the intricacies of rotational motion, the more you'll appreciate the elegance and power of this crucial extension of Newton's foundational work. It serves as a reminder that understanding the world demands moving beyond the simple and embracing the complexities of rotation.
Latest Posts
Latest Posts
-
How Do Water Particles Move In A Wave
Apr 06, 2025
-
Why Is Density An Intensive Property
Apr 06, 2025
-
Which Of The Following Bones Belong To The Axial Skeleton
Apr 06, 2025
-
What Are The Properties Of Solids
Apr 06, 2025
-
Trends In The Periodic Table Answer Key
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Newton's Second Law In Rotational Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
