Polynomial Long Division Worksheet With Answers Pdf
Muz Play
Mar 31, 2025 · 5 min read
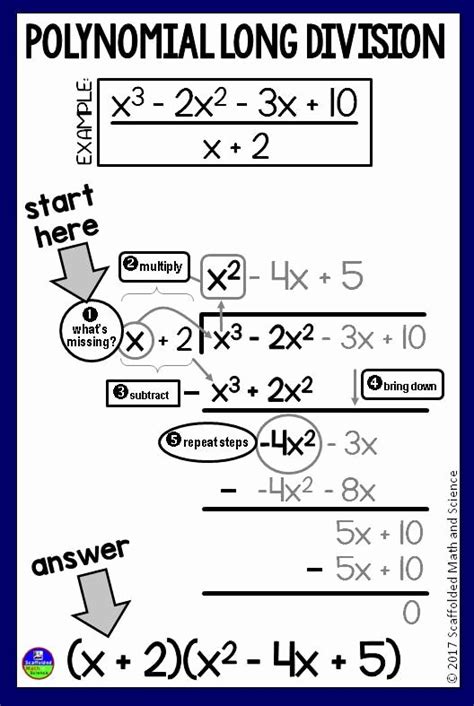
Table of Contents
Polynomial Long Division Worksheet with Answers PDF: A Comprehensive Guide
Polynomial long division is a crucial algebraic skill, forming the bedrock for more advanced concepts in mathematics. Mastering this technique is essential for success in algebra, calculus, and beyond. While textbooks and online resources provide theoretical explanations, practical application through worksheets is key to solidifying understanding. This article serves as a comprehensive guide to polynomial long division, offering explanations, examples, and even strategies for creating your own effective worksheets. We'll also explore where to find readily available worksheets with answers in PDF format.
Understanding Polynomial Long Division
Before diving into worksheets, let's refresh our understanding of the process. Polynomial long division is analogous to long division with numbers. The goal is to divide a polynomial (the dividend) by another polynomial (the divisor) to obtain a quotient and a remainder. The general form is:
Dividend = (Divisor × Quotient) + Remainder
This process involves several steps:
Step-by-Step Guide to Polynomial Long Division
-
Arrange the Polynomials: Ensure both the dividend and divisor are written in descending order of powers of the variable (e.g., x³, x², x, constant). Include zero coefficients for any missing terms to maintain place value.
-
Divide the Leading Terms: Divide the leading term of the dividend by the leading term of the divisor. This result becomes the first term of the quotient.
-
Multiply and Subtract: Multiply the obtained quotient term by the entire divisor. Subtract this product from the dividend.
-
Bring Down the Next Term: Bring down the next term from the dividend.
-
Repeat: Repeat steps 2-4 until the degree of the remaining polynomial (remainder) is less than the degree of the divisor.
Example: Polynomial Long Division
Let's divide (3x³ + 5x² - 7x + 2) by (x + 2):
- Setup:
x + 2 | 3x³ + 5x² - 7x + 2
-
Divide Leading Terms: 3x³ / x = 3x² (This is the first term of the quotient)
-
Multiply and Subtract: 3x²(x + 2) = 3x³ + 6x². Subtracting this from the dividend gives:
x + 2 | 3x³ + 5x² - 7x + 2
- (3x³ + 6x²)
---------------
-x² - 7x
-
Bring Down: Bring down the -7x.
-
Repeat: -x²/x = -x (next term of the quotient). Multiply and subtract:
x + 2 | 3x³ + 5x² - 7x + 2
- (3x³ + 6x²)
---------------
-x² - 7x
- (-x² -2x)
-------------
-5x + 2
- Repeat Again: -5x/x = -5 (next term). Multiply and subtract:
x + 2 | 3x³ + 5x² - 7x + 2
- (3x³ + 6x²)
---------------
-x² - 7x
- (-x² -2x)
-------------
-5x + 2
- (-5x -10)
-----------
12
- Remainder: The remainder is 12.
Therefore, (3x³ + 5x² - 7x + 2) / (x + 2) = 3x² - x - 5 + 12/(x + 2)
Creating Your Own Polynomial Long Division Worksheet
Designing your own worksheet allows for customization based on specific learning needs. Here's a step-by-step guide:
-
Determine the Difficulty Level: Start with simpler problems involving monomial divisors and gradually increase the complexity with binomial and trinomial divisors. Vary the degrees of the polynomials as well.
-
Choose the Problems: Select problems that showcase different aspects of polynomial long division, including cases with remainders and without. Incorporate problems with missing terms to test the understanding of place value.
-
Design the Worksheet: Create a clear and organized layout. Number the problems sequentially. Provide ample space for students to perform calculations. Consider incorporating visual cues or hints if needed.
-
Add Answer Key: This is crucial for self-checking and reinforces learning. Ensure that the answers are meticulously accurate. Consider using a separate answer key sheet to avoid confusion.
-
Consider Different Formats: Explore different problem styles; some examples include:
- Fill-in-the-blanks: Guide students by providing some steps and asking them to complete the rest.
- Multiple Choice: Present students with possible quotients and remainders, encouraging them to choose the correct answer.
- Word Problems: Translate real-world scenarios into polynomial division problems, improving application skills.
Where to Find Polynomial Long Division Worksheets with Answers (PDF)
While creating your own is highly recommended, many readily available resources offer pre-made worksheets:
-
Educational Websites: Numerous websites dedicated to educational resources offer free and printable worksheets, often including answers. Search for "polynomial long division worksheet PDF" on your preferred search engine. Many educational platforms provide differentiated worksheets catering to various skill levels.
-
Textbook Resources: Many algebra textbooks include supplementary worksheets and exercises in their online resources. Check the resources associated with your textbook.
Tips for Effective Learning using Worksheets
-
Practice Regularly: Consistent practice is key to mastering polynomial long division. Work through several problems daily to reinforce your understanding.
-
Review Mistakes: Don't just focus on correct answers. Carefully analyze your mistakes to understand where you went wrong and how to avoid similar errors in the future.
-
Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or classmates if you encounter difficulties. Clarifying doubts promptly prevents misconceptions from solidifying.
-
Use Different Resources: Utilizing a variety of worksheets from different sources exposes you to diverse problem styles and techniques.
Advanced Applications of Polynomial Long Division
Polynomial long division extends far beyond basic algebraic manipulation. It finds applications in:
-
Calculus: Finding derivatives and integrals often involves polynomial division.
-
Partial Fraction Decomposition: This technique relies heavily on polynomial long division for simplifying complex rational expressions.
-
Engineering and Science: Many engineering and scientific applications require manipulating polynomial expressions, and long division proves essential.
Conclusion
Polynomial long division is a fundamental algebraic skill with far-reaching applications. By utilizing worksheets effectively, students can build a strong foundation and master this crucial technique. Remember to practice regularly, review mistakes, and explore various resources to enhance your understanding. Whether you create your own worksheet or download one, consistent practice is the key to success. By focusing on clear explanations, diverse problem types, and ample practice opportunities, you can effectively learn and apply this critical mathematical skill. Remember to always check your answers meticulously and seek clarification when needed. Good luck!
Latest Posts
Latest Posts
-
External Parts Of A Computer System
Apr 01, 2025
-
Is Covalent Bond Between Two Nonmetals
Apr 01, 2025
-
Do Porifera Have A Digestive System
Apr 01, 2025
-
Competing Visions A History Of California
Apr 01, 2025
-
What Are Three Main Ideas Of The Cell Theory
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Polynomial Long Division Worksheet With Answers Pdf . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
