Power Series Of 1 1 X
Muz Play
May 12, 2025 · 5 min read
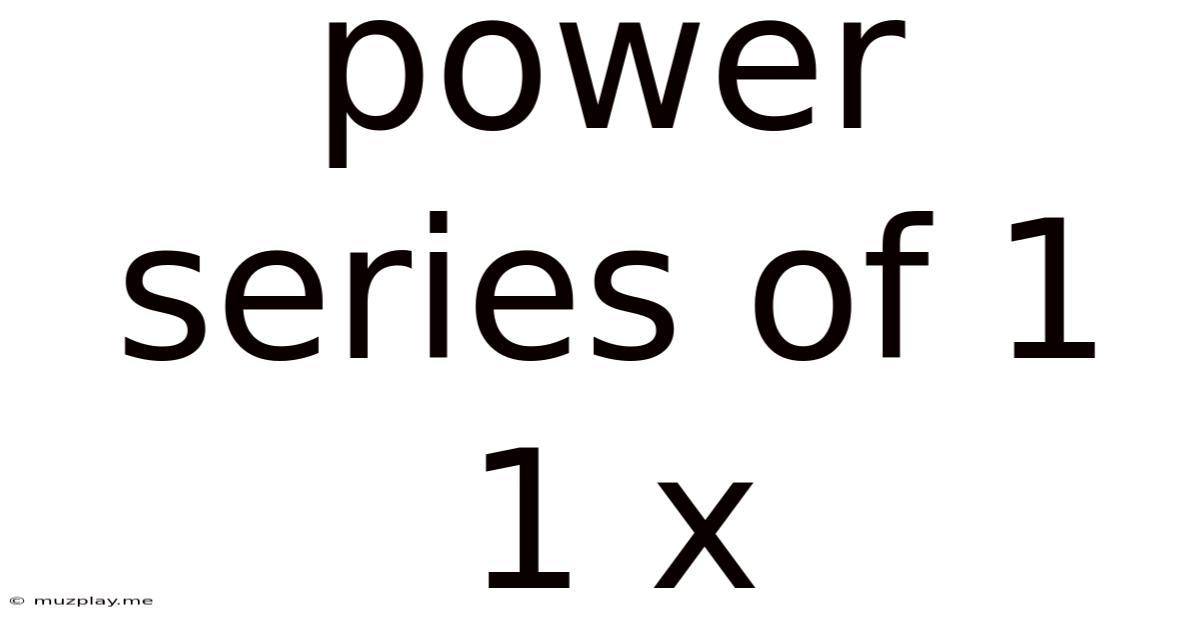
Table of Contents
Power Series Representation of 1/(1-x)
The function 1/(1-x) is a cornerstone in the study of power series. Its simple form belies its profound importance, serving as a generating function for numerous sequences and a foundational element in deriving power series representations for other functions. This article will delve deeply into the power series representation of 1/(1-x), exploring its derivation, radius of convergence, applications, and connections to other mathematical concepts.
Deriving the Power Series: Geometric Series
The most straightforward method to derive the power series for 1/(1-x) is through the geometric series formula. Recall that a geometric series is a series of the form:
a + ar + ar² + ar³ + ...
where 'a' is the first term and 'r' is the common ratio. This series converges to a/(1-r) if |r| < 1.
Let's consider the function 1/(1-x). We can express this as a geometric series with a = 1 and r = x. Therefore:
1/(1-x) = 1 + x + x² + x³ + ... (for |x| < 1)
This is the power series representation of 1/(1-x). The series converges to 1/(1-x) only when the absolute value of the common ratio, |x|, is less than 1. This condition defines the interval of convergence.
Radius of Convergence and Interval of Convergence
The radius of convergence (R) of a power series is the distance from the center of the series (in this case, 0) to the nearest point where the series diverges. For the power series of 1/(1-x), the radius of convergence is 1. This means the series converges for all x such that |x| < 1.
The interval of convergence is the interval on the real number line where the power series converges. For 1/(1-x), the interval of convergence is (-1, 1). Let's examine the endpoints:
- x = 1: The series becomes 1 + 1 + 1 + 1 + ..., which clearly diverges.
- x = -1: The series becomes 1 - 1 + 1 - 1 + ..., which also diverges (it's a Grandi's series).
Therefore, the interval of convergence is strictly (-1, 1).
Techniques for Finding the Power Series
While the geometric series approach is the simplest, other methods can also be used to derive the power series for 1/(1-x):
1. Using the Taylor Series Expansion
The Taylor series expansion of a function f(x) around a point 'a' is given by:
f(x) = Σ [f⁽ⁿ⁾(a)/n!] * (x-a)ⁿ
where f⁽ⁿ⁾(a) is the nth derivative of f(x) evaluated at x = a.
For f(x) = 1/(1-x) and a = 0, we can find the derivatives:
- f(0) = 1
- f'(x) = 1/(1-x)² => f'(0) = 1
- f''(x) = 2/(1-x)³ => f''(0) = 2
- f'''(x) = 6/(1-x)⁴ => f'''(0) = 6
- ...and so on.
Substituting these into the Taylor series formula, we get:
1/(1-x) = 1 + x + x² + x³ + ...
which is the same result as obtained using the geometric series method. This demonstrates the equivalence between the geometric series and the Taylor series expansion in this specific case.
2. Using Long Division
While less elegant, performing long division of 1 by (1-x) can also yield the power series:
1 + x + x² + x³ + ...
------------------------
1-x | 1
1 - x
------
x
x - x²
------
x²
x² - x³
------
x³
...
This process continues indefinitely, generating the same power series.
Applications of the Power Series
The power series representation of 1/(1-x) has far-reaching applications in various fields of mathematics and science:
1. Calculus: Integration and Differentiation
The power series can be integrated and differentiated term by term within the interval of convergence. This allows us to find power series representations for other functions. For example, integrating 1/(1-x) term by term yields the power series for -ln|1-x|.
2. Probability: Generating Functions
In probability theory, power series are used as generating functions. The coefficients of the power series represent probabilities associated with a random variable. The power series for 1/(1-x) is the generating function for a geometric distribution.
3. Physics: Solving Differential Equations
Power series are a powerful tool for solving differential equations, particularly those that don't have closed-form solutions. The power series for 1/(1-x) can serve as a building block in solving more complex equations.
4. Complex Analysis: Laurent Series
In complex analysis, the power series extends to Laurent series, which can represent functions with singularities. The function 1/(1-z) in the complex plane has a singularity at z=1, and its Laurent series representation near this singularity provides valuable information about its behavior.
Extensions and Variations
The basic power series 1/(1-x) can be extended and modified to represent a wider range of functions:
1. 1/(1+x)
Replacing 'x' with '-x' in the original power series gives:
1/(1+x) = 1 - x + x² - x³ + ... (for |x| < 1)
This is an alternating geometric series.
2. 1/(a-x) and 1/(1-ax)
By factoring out constants and appropriate substitutions, we can derive power series for functions like 1/(a-x) and 1/(1-ax).
3. Functions with More Complex Denominators
Through algebraic manipulations and partial fraction decomposition, more complex rational functions can be expressed as sums of simpler fractions, each representable by a power series.
Conclusion
The power series representation of 1/(1-x) is a fundamental concept in mathematics with wide-ranging applications. Its derivation through geometric series and Taylor series provides a solid theoretical foundation, while its applications in calculus, probability, physics, and complex analysis highlight its practical significance. The simplicity of its form belies its power as a building block for understanding and solving more complex mathematical problems. Understanding this power series is essential for anyone pursuing advanced studies in mathematics, science, and engineering. Its versatility and significance make it a key concept worthy of thorough study and appreciation.
Latest Posts
Latest Posts
-
How To Do Bohr Rutherford Diagrams
May 12, 2025
-
Is Milk Pure Substance Or Mixture
May 12, 2025
-
Power Series Of 1 1 X
May 12, 2025
-
Is Boron Trifluoride Polar Or Nonpolar
May 12, 2025
-
Which Point Of The Beam Experiences The Most Compression
May 12, 2025
Related Post
Thank you for visiting our website which covers about Power Series Of 1 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.