Rate Of Change Positive And Decreasing
Muz Play
Mar 26, 2025 · 5 min read
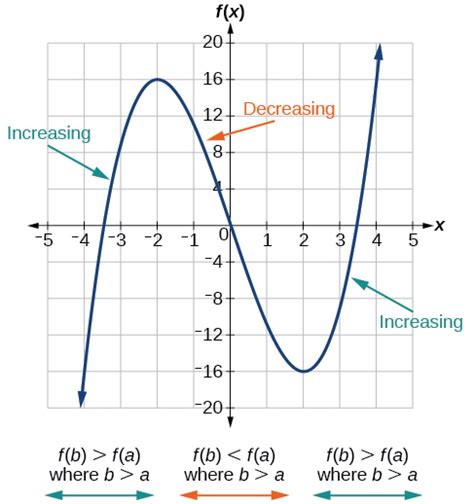
Table of Contents
Rates of Change: Understanding Positive and Decreasing Trends
Rates of change are fundamental concepts in mathematics, science, economics, and numerous other fields. They describe how a quantity changes over time or in relation to another variable. Understanding the difference between positive and decreasing rates of change is crucial for interpreting data, making predictions, and solving problems across various disciplines. This article will delve deep into the concept, exploring its applications and providing practical examples.
What is a Rate of Change?
A rate of change measures how much a quantity changes compared to the change in another quantity, usually time. It's essentially the slope of a function when graphed. We can express it as:
Rate of Change = (Change in Dependent Variable) / (Change in Independent Variable)
The dependent variable is the quantity that changes in response to the independent variable. For instance, if we're tracking the growth of a plant, the height of the plant (dependent variable) changes over time (independent variable).
Positive Rate of Change
A positive rate of change indicates that the dependent variable increases as the independent variable increases. Graphically, this manifests as an upward-sloping line. The steeper the slope, the faster the rate of increase.
Examples:
- Population Growth: A positive rate of change in population means the population is increasing over time.
- Company Profits: If a company's profits are increasing year over year, it shows a positive rate of change in profitability.
- Investment Growth: A positive rate of change in investment value indicates that the investment is growing.
- Temperature Rise: A positive rate of change in temperature signifies that the temperature is increasing.
Decreasing Rate of Change (Negative Rate of Change)
A decreasing rate of change (often referred to as a negative rate of change) signifies that the dependent variable decreases as the independent variable increases. Graphically, this is represented by a downward-sloping line. Again, the steeper the slope, the faster the rate of decrease.
Examples:
- Population Decline: A negative rate of change in population means the population is decreasing over time.
- Depreciation of Assets: The value of assets like cars or machinery typically decreases over time, showcasing a negative rate of change.
- Cooling of an Object: As an object cools, its temperature decreases, illustrating a negative rate of change.
- Debt Reduction: If you are paying off a debt, the amount owed is decreasing, indicating a negative rate of change.
Calculating Rates of Change
Calculating the rate of change involves determining the change in the dependent variable and dividing it by the change in the independent variable. Let's consider a few scenarios:
Scenario 1: Constant Rate of Change (Linear Function)
Imagine a plant grows 2 cm every week. This is a constant rate of change. We can represent this with a linear function:
Height (cm) = 2 * Time (weeks)
The rate of change is a constant 2 cm/week.
Scenario 2: Variable Rate of Change (Non-Linear Function)
Consider a population that grows exponentially. The rate of change is not constant; it increases over time. This is a non-linear function, often described by exponential equations. The rate of change at any given point would be the slope of the tangent line to the curve at that point. Calculus provides the tools to calculate these instantaneous rates of change.
Scenario 3: Average Rate of Change
Often, we only have data points, not a continuous function. In such cases, we calculate the average rate of change between two points.
Let's say a company's profit increased from $10,000 to $15,000 over two years.
Average Rate of Change = ($15,000 - $10,000) / (2 years - 0 years) = $2,500/year
This represents the average annual increase in profit.
Real-World Applications
The concept of rate of change finds applications in a wide range of fields:
1. Economics:
- Economic Growth: Monitoring GDP growth rates.
- Inflation: Measuring the rate at which prices are increasing.
- Unemployment: Tracking changes in the unemployment rate.
- Stock Market: Analyzing changes in stock prices.
2. Science:
- Physics: Calculating velocity (rate of change of displacement) and acceleration (rate of change of velocity).
- Chemistry: Determining reaction rates.
- Biology: Studying population growth and decay.
- Meteorology: Analyzing changes in temperature, pressure, and wind speed.
3. Engineering:
- Structural Engineering: Analyzing rates of stress and strain on materials.
- Mechanical Engineering: Determining the rate of change of machine parts during operation.
4. Medicine:
- Pharmacology: Monitoring drug absorption and elimination rates.
- Epidemiology: Tracking the spread of diseases.
5. Environmental Science:
- Climate Change: Analyzing rates of sea level rise, temperature increase, and greenhouse gas emissions.
- Pollution Control: Monitoring changes in pollutant levels.
Interpreting Rates of Change
The interpretation of a rate of change depends heavily on the context. A positive rate of change might be desirable in some situations (e.g., increasing profits) but undesirable in others (e.g., rising inflation). Similarly, a negative rate of change can be positive (e.g., decreasing debt) or negative (e.g., declining population).
It's crucial to consider the magnitude of the rate of change. A small positive rate of change might be insignificant, while a large negative rate of change could indicate a serious problem. Moreover, the trend is important. A consistently positive rate of change signifies sustained growth, whereas a fluctuating rate of change may suggest instability.
Advanced Concepts
For more in-depth analysis of rates of change, particularly with non-linear functions, the concepts of derivatives and integrals from calculus are essential. Derivatives provide the instantaneous rate of change at a specific point on a curve, while integrals calculate the cumulative change over an interval.
Furthermore, understanding differential equations becomes crucial when modelling dynamic systems where the rate of change is itself a function of other variables.
Conclusion
Rates of change are a fundamental concept with far-reaching implications. Understanding both positive and decreasing rates of change is essential for interpreting data, making informed decisions, and solving problems in various fields. From simple linear calculations to complex calculus-based analyses, the ability to understand and interpret rates of change is a crucial skill in many professions and daily life. Whether you're analyzing financial data, studying scientific phenomena, or simply tracking personal progress, grasping this concept is invaluable. By carefully considering the context, magnitude, and trends of rates of change, we can gain crucial insights into the dynamics of the world around us.
Latest Posts
Latest Posts
-
Plasma Membranes Are Selectively Permeable What Does This Mean
Mar 29, 2025
-
Shape Defined By Color Or Line
Mar 29, 2025
-
Quantitative Analysis Of Vinegar Via Titration
Mar 29, 2025
-
Definition Of Order Of A Reaction
Mar 29, 2025
-
Why Is Blood Clotting A Positive Feedback
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Rate Of Change Positive And Decreasing . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
