Speed Of A Wave On A String
Muz Play
Mar 31, 2025 · 5 min read
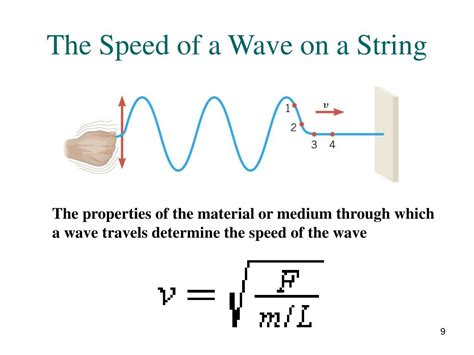
Table of Contents
The Speed of a Wave on a String: A Comprehensive Guide
Understanding the speed of a wave on a string is fundamental to various fields, from music theory and instrument design to telecommunications and seismology. This comprehensive guide delves into the physics behind wave propagation on a string, exploring the factors that influence its speed, the mathematical derivation of the wave speed equation, and practical applications. We'll cover everything from the basic concepts to more advanced considerations, ensuring a thorough understanding for both beginners and those seeking a deeper dive.
Factors Affecting Wave Speed on a String
The speed at which a wave travels along a string depends primarily on two factors: tension and linear mass density.
1. Tension (T):
Tension refers to the force pulling on the string. Imagine pulling on both ends of a guitar string; this force is the tension. The higher the tension, the faster the wave travels. This is intuitive: a tighter string vibrates more quickly, resulting in a higher wave speed. Think of a tightly strung violin string versus a loosely strung one – the tightly strung string produces a higher pitch, indicating a faster wave speed.
2. Linear Mass Density (μ):
Linear mass density (μ) represents the mass per unit length of the string. It's calculated as:
μ = mass (m) / length (L)
The lower the linear mass density, the faster the wave travels. A thinner string with the same mass as a thicker string will have a lower linear mass density, resulting in a faster wave speed. This explains why thinner strings on a guitar or piano produce higher pitches.
The Wave Speed Equation: Deriving the Formula
The relationship between wave speed (v), tension (T), and linear mass density (μ) is described by the following equation:
v = √(T/μ)
This equation is derived from fundamental principles of physics, specifically Newton's second law and the concept of wave propagation. Let's explore a simplified derivation:
Consider a small segment of the string, of length Δx, undergoing transverse wave motion. The mass of this segment is μΔx. The restoring force acting on this segment is approximately equal to the difference in tension between the two ends of the segment. For small angles of displacement, this force is proportional to the curvature of the string, which in turn is related to the second derivative of the string's displacement with respect to position.
Applying Newton's second law (F = ma), where the acceleration is the second partial derivative of the displacement with respect to time, we can establish a second-order partial differential equation that describes the wave motion. Solving this equation using standard techniques leads to the wave speed equation: v = √(T/μ).
Practical Applications and Examples
The speed of a wave on a string has numerous applications across various disciplines:
1. Musical Instruments:
The pitch of a musical instrument string is directly related to the speed of the wave traveling along it. Higher wave speed implies higher frequency and hence a higher pitch. Instrument makers carefully select string materials and tensions to achieve the desired pitch and tone. Different string gauges (thickness) are used to create different registers in a musical instrument, manipulating the linear mass density.
2. Telecommunications:
In early telecommunication systems, sound waves were transmitted along wires using mechanical vibrations. The speed of these waves, determined by the tension and mass density of the wires, played a crucial role in determining the fidelity and speed of transmission. While modern telecommunications use electrical signals, the underlying principles remain relevant in understanding wave propagation in transmission media.
3. Seismology:
Seismic waves, which travel through the Earth after an earthquake, have characteristics analogous to waves on a string. While the medium is vastly different, the speed of seismic waves is determined by the elastic properties and density of the Earth's materials, analogous to tension and mass density in a string. Understanding seismic wave speeds is crucial for earthquake location and the study of Earth's interior structure.
4. Measuring Tension:
The wave speed equation can be used to indirectly measure tension in a string. By measuring the wave speed (for example, using the frequency of a standing wave) and knowing the linear mass density, the tension can be calculated. This technique is utilized in various engineering and physics experiments.
Advanced Considerations and Beyond the Basics
While the equation v = √(T/μ) provides a good approximation for wave speed on a string, several factors can influence the accuracy of this calculation:
-
String stiffness: The basic equation assumes a perfectly flexible string. However, real strings possess some stiffness, which affects the wave speed, especially at higher frequencies. The stiffer the string, the faster the wave will travel at high frequencies.
-
Damping: Energy is lost due to friction and air resistance, resulting in damping of the wave. Damping reduces the amplitude of the wave as it propagates, and over time, affects the measured wave speed. This is especially relevant for waves traveling over long distances.
-
Non-linear effects: At high amplitudes, the wave motion becomes non-linear, meaning the wave speed is no longer solely determined by tension and mass density. Non-linear effects introduce complexities to the wave behavior.
-
Temperature: Temperature affects the properties of the string material, influencing both its tension and mass density. Changes in temperature can therefore alter the wave speed.
-
String Material: The material properties of the string itself influence wave speed beyond its simple mass and density. Factors like elasticity and internal friction can affect how quickly a wave travels.
Understanding these advanced considerations is crucial for accurate modeling and prediction of wave behavior in real-world scenarios.
Conclusion: Mastering the Speed of Waves on a String
The speed of a wave on a string is a fundamental concept with far-reaching implications across numerous scientific and engineering disciplines. The simple equation v = √(T/μ) provides a good starting point for understanding this phenomenon. However, for more accurate predictions, it's essential to consider the various factors that can affect wave propagation, including string stiffness, damping, non-linear effects, and temperature variations. By understanding these complexities, one can gain a deeper appreciation of the physics behind wave motion and its diverse applications. This knowledge is crucial for anyone working with vibrating strings, from musicians and instrument designers to engineers and physicists. Further exploration of these advanced concepts will lead to a more complete understanding of this fundamental aspect of wave physics.
Latest Posts
Latest Posts
-
The Most Reactive Group In The Periodic Table
Apr 02, 2025
-
How To Write Quadratic Equation From Graph
Apr 02, 2025
-
How To Place A Condom Catheter
Apr 02, 2025
-
How Many Elements Are Gases At Room Temperature
Apr 02, 2025
-
3 Main Ideas Of Cell Theory
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Speed Of A Wave On A String . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
