The Mean Of The Sampling Distribution Is Given By
Muz Play
Apr 06, 2025 · 6 min read
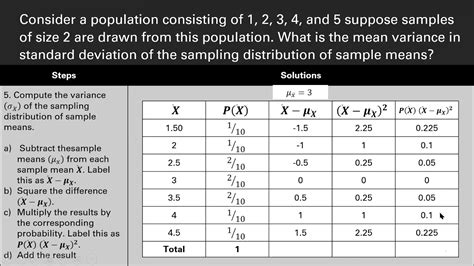
Table of Contents
The Mean of the Sampling Distribution: A Deep Dive
Understanding the mean of the sampling distribution is crucial for anyone working with statistics, particularly in inferential statistics. This concept forms the bedrock of hypothesis testing and confidence intervals, allowing us to draw conclusions about a population based on a sample. This article will provide a comprehensive explanation of the mean of the sampling distribution, exploring its properties, calculations, and practical applications. We will delve into the relationship between the sample mean, the population mean, and the central limit theorem, shedding light on this fundamental statistical principle.
What is a Sampling Distribution?
Before we delve into the mean of the sampling distribution, let's clarify what a sampling distribution actually is. Imagine you have a large population, say, the heights of all adults in a country. Measuring the height of every single individual would be incredibly time-consuming and expensive. Instead, we take a sample – a smaller, manageable subset of the population. We calculate the mean height of this sample. Now, imagine repeating this process numerous times – taking many different samples of the same size from the same population and calculating the mean of each sample. The collection of all these sample means forms the sampling distribution of the sample mean.
This isn't just a collection of random numbers; it follows a specific probability distribution, characterized by its own mean and standard deviation. Understanding this distribution is vital because it allows us to make inferences about the population mean based on the sample mean we obtain.
The Mean of the Sampling Distribution: Unveiling the Expectation
The mean of the sampling distribution, often denoted as μ<sub>x̄</sub> (mu sub x-bar), is the average of all possible sample means. This is a crucial concept because it's unbiased: it's an accurate representation of the population mean (μ). This means that:
μ<sub>x̄</sub> = μ
This simple equation is powerful. It states that if you were to take countless samples and average all their means, you would arrive at the true population mean. This property is fundamental to the logic behind statistical inference. We use the sample mean (x̄) as an estimator of the population mean (μ), and the fact that μ<sub>x̄</sub> = μ assures us that this estimator is unbiased; it doesn't systematically overestimate or underestimate the true value.
Proof of Unbiasedness: A Glimpse into Mathematical Statistics
While a full mathematical proof requires a deeper understanding of expectation and random variables, we can illustrate the concept intuitively. Consider a simple scenario where we're drawing samples from a population with known mean (μ) and standard deviation (σ). Each sample mean (x̄) will fluctuate around the population mean. Some will be higher, some lower. However, because of the central limit theorem (discussed later), the positive and negative deviations will largely cancel each other out when we average all the sample means. The net effect is that the average of all sample means converges to the population mean.
Standard Error: Measuring the Variability
The mean of the sampling distribution tells us the central tendency of the sample means, but it doesn't tell us anything about their variability. This variability is quantified by the standard error (SE), often written as σ<sub>x̄</sub> (sigma sub x-bar). The standard error is the standard deviation of the sampling distribution. It measures how much the sample means tend to vary from the population mean. A smaller standard error indicates that the sample means cluster tightly around the population mean, while a larger standard error indicates more variability.
The standard error is calculated as:
σ<sub>x̄</sub> = σ / √n
where:
- σ is the population standard deviation
- n is the sample size
This formula highlights the inverse relationship between sample size and standard error. Larger sample sizes lead to smaller standard errors, indicating that larger samples provide more precise estimates of the population mean.
The Central Limit Theorem: A Cornerstone of Statistical Inference
The central limit theorem (CLT) is a cornerstone of statistical inference, and it's directly related to the properties of the sampling distribution. The CLT states that, regardless of the shape of the population distribution, the sampling distribution of the sample mean will approach a normal distribution as the sample size (n) increases. This is true even if the original population distribution is skewed or non-normal.
The CLT has several crucial implications:
- Normality: It allows us to utilize the properties of the normal distribution to make inferences about the population mean, even when the population distribution is unknown.
- Approximation: Even with moderately sized samples (generally considered n ≥ 30), the sampling distribution is often sufficiently close to a normal distribution for practical purposes.
- Standard Error: The standard error becomes increasingly smaller with larger sample sizes, meaning our estimates of the population mean become increasingly precise.
Practical Applications and Examples
The concepts discussed have wide-ranging applications across various fields:
- Hypothesis Testing: We use the sampling distribution to determine the probability of observing a sample mean as extreme as the one obtained if the null hypothesis is true.
- Confidence Intervals: We construct confidence intervals to estimate a range of values within which the population mean likely falls, based on the sample mean and the standard error.
- Quality Control: In manufacturing, sampling distributions help assess the quality of products by estimating the mean of a quality characteristic from samples.
- Medical Research: In clinical trials, sampling distributions are used to compare the effectiveness of treatments by analyzing the mean differences in outcomes between treatment and control groups.
- Market Research: Sampling distributions allow market researchers to estimate population preferences or behaviors based on surveys of samples from the target market.
Example: Estimating Average Income
Let's say we want to estimate the average annual income of households in a city. We take a random sample of 100 households and calculate their average income (x̄). The standard deviation of incomes in the sample (s) is $10,000. We can estimate the standard error as:
SE = s / √n = $10,000 / √100 = $1000
This standard error represents the uncertainty in our estimate of the average income. A smaller standard error would indicate greater confidence in our estimate. Knowing the standard error allows us to construct a confidence interval around the sample mean to estimate the range within which the true average household income likely lies.
Conclusion: The Importance of Understanding Sampling Distributions
The mean of the sampling distribution, its relationship with the population mean, and the concept of standard error are fundamental to statistical inference. Understanding these concepts allows us to make informed decisions based on sample data, even without complete knowledge of the entire population. The central limit theorem plays a pivotal role, allowing us to leverage the properties of the normal distribution regardless of the original data's distribution. These principles are widely applicable across numerous fields, making a solid grasp of sampling distributions essential for anyone working with data analysis and statistical inference. The ability to interpret and use this information allows for stronger conclusions, more informed decisions, and a more nuanced understanding of the world around us.
Latest Posts
Latest Posts
-
Calculating Heat Of Reaction From Bomb Calorimetry Data
Apr 08, 2025
-
What Is The Iupac Name For This Alkane
Apr 08, 2025
-
How To Interpret Post Hoc Test
Apr 08, 2025
-
Collection Of Nerve Cell Bodies In The Peripheral Nervous System
Apr 08, 2025
-
Which Of The Following Is True Of Spending In Politics
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about The Mean Of The Sampling Distribution Is Given By . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.