The Metric System Is Based On Powers Of
Muz Play
Apr 06, 2025 · 6 min read
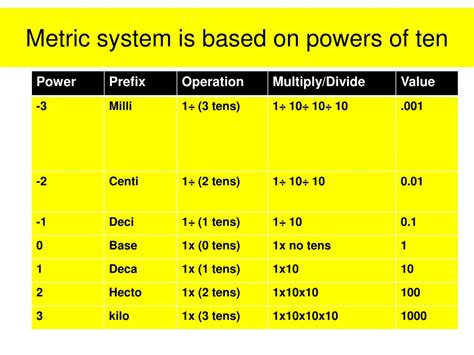
Table of Contents
The Metric System is Based on Powers of 10: A Deep Dive into Decimal Simplicity
The metric system, formally known as the International System of Units (SI), reigns supreme as the world's most widely used system of measurement. Its enduring popularity stems from its inherent elegance and simplicity: it's based on powers of 10. This seemingly small detail revolutionized measurement, offering unparalleled ease of use and conversion compared to its imperial counterpart. This article delves deep into the foundational principles of the metric system, exploring how its reliance on powers of 10 streamlines calculations, facilitates scientific collaboration, and contributes to its global dominance.
Understanding the Power of Ten
Before exploring the metric system's intricacies, let's solidify our understanding of powers of 10. A power of 10 is simply 10 multiplied by itself a certain number of times. This "certain number" is represented by an exponent. For instance:
- 10<sup>0</sup> = 1 (Any number raised to the power of 0 equals 1)
- 10<sup>1</sup> = 10
- 10<sup>2</sup> = 100
- 10<sup>3</sup> = 1000
- 10<sup>-1</sup> = 0.1 (Negative exponents represent fractions or decimals)
- 10<sup>-2</sup> = 0.01
- 10<sup>-3</sup> = 0.001
Notice the pattern: each increase in the exponent adds another zero to the number. Similarly, each decrease in the exponent adds another zero after the decimal point. This consistent relationship is the key to the metric system's efficiency.
The Metric System's Base Units
The metric system's brilliance lies in its use of seven base units, each representing a fundamental physical quantity. These are:
- Meter (m): The base unit of length. Imagine a meter stick – a fundamental tool for measuring distances.
- Kilogram (kg): The base unit of mass. Note that the kilogram is unique; it's the only base unit with a prefix (kilo).
- Second (s): The base unit of time. This is arguably the most universally understood base unit.
- Ampere (A): The base unit of electric current. This reflects the system's capacity to encompass various scientific disciplines.
- Kelvin (K): The base unit of thermodynamic temperature.
- Mole (mol): The base unit of amount of substance. This is vital in chemistry and related fields.
- Candela (cd): The base unit of luminous intensity. This is crucial for measuring light.
These base units are the building blocks of the entire system. All other metric units are derived from these seven. The consistent use of powers of 10 simplifies the relationship between these derived units.
Prefixes: The Key to Decimal Conversion
The metric system employs a series of prefixes to indicate multiples and submultiples of the base units. These prefixes, all based on powers of 10, are crucial for expressing measurements across vast scales. Here are some of the most commonly used prefixes:
| Prefix | Symbol | Power of 10 | Prefix | Symbol | Power of 10 | |
|---|---|---|---|---|---|---|
| Giga | G | 10<sup>9</sup> | milli | m | 10<sup>-3</sup> | |
| Mega | M | 10<sup>6</sup> | micro | µ | 10<sup>-6</sup> | |
| Kilo | k | 10<sup>3</sup> | nano | n | 10<sup>-9</sup> | |
| Hecto | h | 10<sup>2</sup> | pico | p | 10<sup>-12</sup> | |
| Deca | da | 10<sup>1</sup> | femto | f | 10<sup>-15</sup> | |
| atto | a | 10<sup>-18</sup> |
Example: A kilometer (km) is 1000 meters (10<sup>3</sup> m), while a millimeter (mm) is 0.001 meters (10<sup>-3</sup> m). This simple relationship allows for effortless conversion between units. To convert kilometers to millimeters, you simply multiply by 10<sup>6</sup> (1000 x 1000).
Advantages of the Power of 10 Basis
The consistent use of powers of 10 in the metric system offers a multitude of advantages:
- Simplicity of Conversion: Converting between units is straightforward; it involves only moving the decimal point. No complex fractions or multiplication factors are needed.
- Ease of Calculation: Scientific calculations become significantly easier because all units are related by powers of 10. This simplifies calculations involving different units of measurement.
- Global Standardization: The widespread adoption of the metric system facilitates international collaboration in science, engineering, and commerce. Everyone uses the same system, eliminating the need for cumbersome unit conversions.
- Consistency and Clarity: The system's inherent logic minimizes errors and misunderstandings. The clear and consistent relationships between units prevent ambiguity.
- Adaptability to Diverse Scales: From measuring subatomic particles to astronomical distances, the metric system's prefixes effectively handle measurements across an enormous range of scales.
Comparison with the Imperial System
The imperial system, used primarily in the United States, lacks the elegant simplicity of the metric system. Its inconsistent units and complex conversion factors make calculations cumbersome and prone to errors. For example, converting inches to feet, yards to miles, or ounces to pounds requires remembering different conversion factors, a process significantly more error-prone than the straightforward decimal shifts in the metric system.
Applications Across Various Fields
The metric system's versatility extends across numerous disciplines:
- Science and Engineering: The metric system's precision and consistency are essential for accurate scientific measurements and engineering calculations. The ease of conversion and calculation minimizes errors in research and development.
- Medicine: Precise measurements are critical in healthcare, making the metric system's accuracy indispensable for dosage calculations and patient monitoring.
- Manufacturing: Standardized measurements are crucial for manufacturing efficiency and quality control. The metric system ensures uniformity in production across different countries.
- International Trade: The global adoption of the metric system promotes smooth international trade by eliminating the need for unit conversions in import and export operations.
- Everyday Life: While the imperial system persists in some regions, the metric system is increasingly used in everyday life, from grocery shopping to cooking. The intuitive nature of the system makes it user-friendly for people of all backgrounds.
The Future of the Metric System
The metric system's dominance is unlikely to diminish. Its inherent simplicity, precision, and global acceptance make it the ideal measurement system for a globally interconnected world. While regional variations and legacy systems may linger, the metric system remains the cornerstone of scientific advancement, international collaboration, and accurate measurement across diverse fields. The future of measurement clearly lies in the continued adoption and refinement of this decimal-based system.
Conclusion: A Legacy of Decimal Simplicity
The metric system's foundation in powers of 10 is not merely a mathematical detail; it's the very essence of its success. This elegant and efficient system offers unmatched simplicity, accuracy, and global standardization, making it the preferred system for scientific, engineering, and everyday applications worldwide. Its enduring legacy lies in its consistent and logical approach to measurement, simplifying calculations, facilitating communication, and promoting a unified global understanding of quantities. The power of 10 isn't just a number; it's the foundation of a system that revolutionized how we measure the world.
Latest Posts
Latest Posts
-
Instrument Used To Measure Length In Science
Apr 07, 2025
-
What Is A Compound Statement In Math
Apr 07, 2025
-
Lattice Energy Is An Estimate Of The Bond
Apr 07, 2025
-
What Are The Similarities Between Animal Cells And Plant Cells
Apr 07, 2025
-
Naming Compounds Practice Problems With Answers
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about The Metric System Is Based On Powers Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
