What Does The Pauli Exclusion Principle State
Muz Play
Mar 30, 2025 · 6 min read
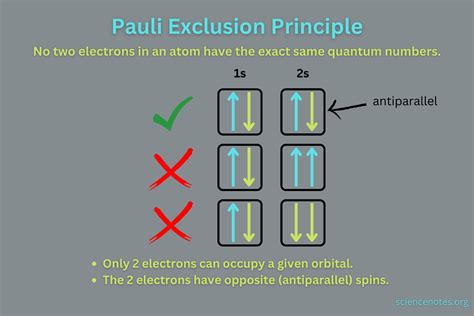
Table of Contents
What Does the Pauli Exclusion Principle State? A Deep Dive into Quantum Mechanics
The Pauli Exclusion Principle, a cornerstone of quantum mechanics, dictates how electrons behave within an atom and, by extension, influences the properties of all matter. It's not just a dry scientific law; it's the fundamental reason why matter occupies space and doesn't collapse into an infinitely small point. Understanding this principle unlocks a deeper appreciation for the intricacies of the universe at the atomic level.
Understanding the Basics: Fermions and the Exclusion Principle
At its core, the Pauli Exclusion Principle states that no two identical fermions can occupy the same quantum state simultaneously. Let's break down this seemingly simple sentence:
-
Identical Fermions: Fermions are a class of particles that includes electrons, protons, and neutrons – the building blocks of ordinary matter. "Identical" means they have the same intrinsic properties, like mass and charge. Crucially, fermions also possess an intrinsic angular momentum called spin. This spin is quantized, meaning it can only take on specific, discrete values.
-
Quantum State: A quantum state describes all the possible properties of a particle. For an electron in an atom, this includes its energy level, orbital angular momentum, magnetic quantum number (related to the orientation of its orbital in space), and spin. These four quantum numbers together uniquely define an electron's state within an atom.
-
Simultaneously: This emphasizes that the exclusion applies at the same time, not just at different points in time. Two electrons cannot occupy the same exact state even for an infinitesimally small period.
Therefore, if you have two electrons in an atom, they must have at least one different quantum number. If they share the same energy level, orbital angular momentum, and magnetic quantum number, their spins must be opposite (+1/2 and -1/2). This directly impacts how electrons fill up atomic orbitals and, consequently, the arrangement of electrons in the periodic table.
The Implications of the Pauli Exclusion Principle
The Pauli Exclusion Principle isn't just an abstract concept; it has profound consequences across various aspects of physics and chemistry:
1. Atomic Structure and the Periodic Table
The principle dictates how electrons are arranged within an atom. Electrons fill the lowest energy levels first, but the exclusion principle prevents them from all collapsing into the same lowest energy state. Instead, they fill higher energy levels and subshells, resulting in the characteristic electron configurations of elements. This is precisely why the periodic table is structured the way it is – it reflects the filling of electron shells and subshells according to the Pauli Exclusion Principle.
The periodic table's arrangement is directly linked to electron configurations which are governed by this fundamental principle. Without it, all electrons would occupy the lowest energy level, making the universe as we know it impossible.
2. Chemical Bonding
The Pauli Exclusion Principle plays a crucial role in determining how atoms interact and form chemical bonds. The sharing or transfer of electrons to achieve stable electron configurations (usually full outer shells) are direct consequences of this principle. For instance, the formation of covalent bonds involves the sharing of electrons between atoms to fill their outermost electron shells, a process strictly governed by the Pauli Exclusion Principle.
The stability of molecules, and therefore the existence of chemical compounds, is strongly influenced by how electrons are arranged and share space; this is a direct result of the principle.
3. Material Properties
The physical and chemical properties of materials are largely determined by their electronic structure. The Pauli Exclusion Principle underpins this structure, influencing everything from the conductivity of metals to the insulating properties of non-metals.
For example, the electrical conductivity of metals is explained by the presence of delocalized electrons that can move freely through the material. This mobility is a consequence of the way electrons are arranged within the metal's atomic structure, a structure dictated by the Pauli Exclusion Principle.
4. Stability of Matter
Perhaps the most striking implication is the stability of matter itself. Without the Pauli Exclusion Principle, electrons would all collapse into the lowest energy level of an atom. Atoms would be far smaller and the universe as we know it would be radically different; likely, unstable and densely packed. The exclusion principle prevents this catastrophic collapse, ensuring that atoms occupy a finite volume of space. This principle is what keeps matter stable and prevents the universe from collapsing.
5. White Dwarf Stars and Neutron Stars
The Pauli Exclusion Principle even has implications on a cosmic scale. In white dwarf stars, the immense gravitational pressure is counteracted by the electron degeneracy pressure – a pressure arising from the Pauli Exclusion Principle. Similarly, in neutron stars, the pressure from neutron degeneracy prevents further collapse. Without the Pauli Exclusion Principle, these celestial bodies would collapse into black holes.
The existence of white dwarf and neutron stars, which are remarkable objects in the universe, is directly related to the principles of degeneracy pressure.
Distinguishing Fermions from Bosons
The Pauli Exclusion Principle applies only to fermions. Another class of particles, called bosons, do not obey this principle. Bosons include photons (light particles), gluons (which mediate the strong nuclear force), and certain composite particles like mesons.
Bosons can all occupy the same quantum state simultaneously. This is the basis for phenomena such as lasers, where many photons occupy the same quantum state, leading to coherent light. The contrasting behavior between fermions and bosons highlights the fundamental differences in their quantum mechanical properties.
Mathematical Formulation
The Pauli Exclusion Principle can be expressed mathematically using the concept of wave functions. For a system of identical fermions, the total wave function must be antisymmetric with respect to the exchange of any two particles. This means that if you swap the coordinates of two fermions in the wave function, the overall sign of the wave function changes. If the wave function were symmetric (no sign change), it would imply that the fermions are in the same quantum state, violating the exclusion principle.
This mathematical formulation provides a rigorous and quantitative description of the principle.
Beyond the Basics: Further Exploration
The Pauli Exclusion Principle is a fundamental principle with far-reaching consequences. Its implications extend beyond what has been discussed here, into areas such as:
- Nuclear Physics: The structure and stability of atomic nuclei are influenced by the Pauli Exclusion Principle applied to protons and neutrons.
- Solid-State Physics: The behavior of electrons in solids, including the formation of energy bands and the electrical conductivity of materials, is governed by this principle.
- Quantum Field Theory: The principle finds a natural place within the framework of quantum field theory, which describes the interactions of particles and fields.
Further exploration into these advanced topics will reveal the even deeper and broader implications of this critical principle.
Conclusion: A Principle of Fundamental Importance
The Pauli Exclusion Principle is not merely a scientific curiosity; it is a fundamental principle that shapes our understanding of the universe. It underpins the structure of matter, governs chemical reactions, and even influences the behavior of celestial bodies. By understanding this principle, we gain a deeper appreciation for the intricate workings of the quantum world and its impact on our macroscopic reality. Its impact on our understanding of the universe is profound and continues to inspire research and discovery in various scientific fields. From the structure of atoms to the behavior of stars, the Pauli Exclusion Principle stands as a testament to the elegance and power of quantum mechanics. Its implications are far-reaching, ensuring that its study remains an active and crucial area of research.
Latest Posts
Latest Posts
-
What Are The Simplest Body Structures Considered Alive
Apr 01, 2025
-
Chi Squared Goodness Of Fit Vs Independence
Apr 01, 2025
-
What Is The Symbol For Momentum
Apr 01, 2025
-
The Shaft Of The Bone Is Called
Apr 01, 2025
-
Van Der Waals Equation Constants A And B
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Does The Pauli Exclusion Principle State . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
