What Is Kf In Freezing Point Depression
Muz Play
Apr 03, 2025 · 6 min read
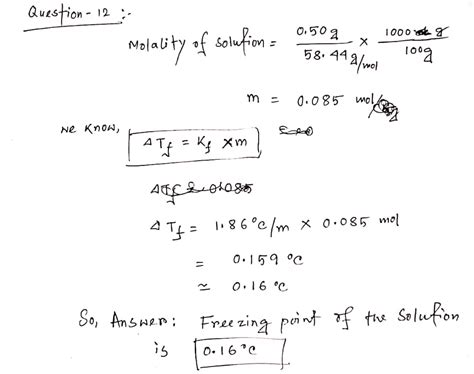
Table of Contents
What is Kf in Freezing Point Depression? A Comprehensive Guide
Freezing point depression is a colligative property, meaning it depends on the concentration of solute particles, not their identity. Understanding this phenomenon is crucial in various fields, from chemistry and physics to food science and cryobiology. A key component of calculating freezing point depression is the cryoscopic constant, often represented as Kf. This article will delve deep into what Kf represents, how it's used, its limitations, and its applications across different disciplines.
Understanding Freezing Point Depression
Before diving into Kf, let's establish a foundational understanding of freezing point depression itself. When a solute is added to a solvent (like dissolving salt in water), the freezing point of the resulting solution is lower than the freezing point of the pure solvent. This happens because the solute particles disrupt the solvent's ability to form a stable solid structure (like ice crystals). The more solute particles present, the greater the disruption, and consequently, the lower the freezing point.
This depression in freezing point is directly proportional to the molality (moles of solute per kilogram of solvent) of the solution. This relationship is expressed mathematically as:
ΔTf = Kf * m * i
Where:
- ΔTf is the change in freezing point (freezing point of pure solvent – freezing point of solution)
- Kf is the cryoscopic constant (specific to the solvent)
- m is the molality of the solution (moles of solute / kg of solvent)
- i is the van't Hoff factor (accounts for the dissociation of solute particles; more on this later)
What is Kf? The Cryoscopic Constant Explained
The cryoscopic constant (Kf) is a proportionality constant that reflects the solvent's inherent resistance to freezing point depression. It's a characteristic property of the solvent and is independent of the solute used. In simpler terms, Kf quantifies how much the freezing point of a solvent will decrease for each molal concentration of solute added.
A higher Kf value indicates that the solvent is more susceptible to freezing point depression; a small amount of solute will significantly lower its freezing point. Conversely, a lower Kf value implies that the solvent is less susceptible.
Kf is typically expressed in units of °C kg/mol or K kg/mol. The value of Kf is determined experimentally for each solvent. Some common solvents and their corresponding Kf values are shown below (note that these values can slightly vary depending on the source and experimental conditions):
- Water: 1.86 °C kg/mol
- Benzene: 5.12 °C kg/mol
- Cyclohexane: 20.0 °C kg/mol
- Camphor: 40.0 °C kg/mol
The Role of Molality (m)
The molality (m) is a crucial factor in calculating freezing point depression. Unlike molarity (moles of solute per liter of solution), molality is based on the mass of the solvent rather than the volume of the solution. This is important because volume can change with temperature, while mass remains constant. Using molality ensures a more accurate and consistent calculation of freezing point depression, irrespective of temperature variations.
Calculating molality involves determining the number of moles of solute and dividing it by the mass of the solvent in kilograms. For example, if you dissolve 0.1 moles of a solute in 0.5 kg of water, the molality is 0.1 mol / 0.5 kg = 0.2 mol/kg or 0.2 m.
The Van't Hoff Factor (i)
The van't Hoff factor (i) accounts for the degree of dissociation or association of a solute in solution. For non-electrolytes (substances that do not dissociate into ions when dissolved), the van't Hoff factor is typically 1. This means each solute particle contributes individually to the depression of the freezing point.
However, for strong electrolytes (like salts that completely dissociate into ions), the van't Hoff factor is greater than 1. For example, NaCl dissociates into two ions (Na⁺ and Cl⁻) in water, so its van't Hoff factor is approximately 2. Similarly, MgCl₂ has a van't Hoff factor of approximately 3.
The van't Hoff factor is an important correction factor because it accounts for the actual number of particles contributing to the colligative property. For weak electrolytes (substances that partially dissociate), the van't Hoff factor is between 1 and the theoretical maximum based on complete dissociation. Its value often needs to be determined experimentally.
Applications of Kf and Freezing Point Depression
The understanding and application of Kf and freezing point depression extend across numerous scientific and practical domains:
1. Determining Molar Mass
Freezing point depression is a widely used method to determine the molar mass of an unknown solute. By measuring the freezing point depression of a solution with a known mass of solute and solvent, one can calculate the molality and, subsequently, the molar mass using the formula:
m = (moles of solute) / (mass of solvent in kg)
moles of solute = (mass of solute) / (molar mass of solute)
Combining these equations with the freezing point depression equation (ΔTf = Kf * m * i) allows the determination of the unknown molar mass.
2. Food Science and Preservation
Freezing point depression is exploited in food preservation. Adding salt or sugar to food lowers its freezing point, preventing the formation of large ice crystals that can damage food texture during freezing. This is why salt is added to ice in ice cream making – lowering the freezing point allows for lower temperatures to be achieved and smoother ice cream production.
3. Cryobiology
Cryobiology deals with the effects of low temperatures on biological systems. Understanding freezing point depression is critical in cryopreservation techniques, where cells and tissues are preserved by freezing. Controlled freezing rates and the use of cryoprotectants (substances that lower the freezing point and reduce ice crystal formation) are crucial for minimizing damage to biological samples.
4. De-icing Agents
The application of salt and other compounds to de-ice roads and runways during winter relies on freezing point depression. These substances lower the freezing point of water, preventing ice formation even at sub-zero temperatures.
5. Physical Chemistry Studies
Kf and freezing point depression are essential tools for studying solute-solvent interactions and the behavior of solutions. Experiments involving freezing point depression can provide valuable insights into the nature of intermolecular forces and the degree of solute dissociation or association.
Limitations and Considerations
While Kf and freezing point depression provide a powerful tool for various applications, some limitations need to be considered:
-
Ideal Solutions: The freezing point depression equation assumes an ideal solution, where solute-solvent interactions are minimal. In reality, deviations from ideality can occur, particularly at higher concentrations, leading to discrepancies in calculated values.
-
Ion Pairing: In electrolyte solutions, ion pairing (where oppositely charged ions associate) can reduce the effective number of particles contributing to freezing point depression, thus affecting the accuracy of the van't Hoff factor.
-
Solubility: The solubility of the solute in the solvent is a limiting factor. If the solute is not completely soluble, the calculated molality will be inaccurate.
-
Experimental Errors: Accurate measurement of the freezing point is crucial for accurate results. Experimental errors in temperature measurement can lead to significant errors in the calculated Kf value or molar mass.
Conclusion
The cryoscopic constant, Kf, is a fundamental constant in understanding and applying the colligative property of freezing point depression. Its significance stretches across numerous scientific and practical fields. While the calculations might seem straightforward, understanding the nuances of ideal solutions, the van't Hoff factor, and the inherent limitations ensures accurate and meaningful applications of this important concept. From determining molar masses to preserving biological samples and de-icing roads, Kf plays a vital, often unseen, role in our daily lives. A thorough understanding of Kf and its implications empowers us to better harness its potential across a wide spectrum of applications.
Latest Posts
Latest Posts
-
What Is The Function Of Nadh And Fadh2
Apr 04, 2025
-
Disadvantages And Advantages Of Sexual Reproduction
Apr 04, 2025
-
Wavelength Of A Helium Neon Laser
Apr 04, 2025
-
How Do You Write Complex Numbers In Standard Form
Apr 04, 2025
-
Shaft Of The Long Bone Is Called
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is Kf In Freezing Point Depression . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
